Геометрия в нашем доме: Проект по математике «Геометрические фигуры в моем доме»

Содержание

Проект по математике «Геометрические фигуры в моем доме»

Муниципальное бюджетное общеобразовательное учреждение Покровская средняя школа

Ухоловского муниципального района Рязанской области 391923,Рязанская область, Ухоловский район, с. Покровское, ул. Школьная, д. 19, тел. 5 -54-10

Тема:

Выполнила ученица 6 класса Воронкова Татьяна

Руководитель: учитель математики Воронкова М.И.

Цели и задачи проекта

Цель

Задачи работы

Изучить теоретические сведения о науке геометрии.
Выделить основные геометрические фигуры.
Выяснить происхождение геометрических фигур.
Изучить сведения о плоских фигурах и объемных.
Провести исследование объектов с целью определения их геометрической формы.

Содержание

Введение

Глава 1. Происхождение геометрии.

1.1 Как возникла геометрия?

1.2 Что изучает геометрия?

1.3 Происхождение геометрических фигур.

Глава 2. Организация исследования.

2.1 Исследование объектов.

2.2 Выбор геометрических форм человеком в повседневной жизни.

2.3 Отличие плоских и объемных геометрических фигур.

2.4 Геометрические фигуры в природе.

Глава 3. Практическая часть.

3.1 Составление дневника наблюдений.

Заключение, выводы

Список использованной литературы

Введение

Каждый замечал как много фигур вокруг. Люди давно заинтересовались их разнообразием, строением и свойствами. Мне тоже стало интересно происхождение геометрических фигур: почему фигуры получили такие названия, где и когда они впервые появились. Еще я заметила, что окружающие нас предметы, похожи на геометрические фигуры. И я решила найти ответы на свои вопросы.

Как возникла геометрия?

Геометрия – одна из древнейших наук. Геометрия (греч. geometria, от geо — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы. Происхождение термина «Геометрия», что буквально означает «землемерие», можно объяснить следующими словами, древнегреческого учёного Евдема Родосского (4 в. до н. э.): «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нила, постоянно смывавшего границы». Она зародилась в Древнем Египте.

В этом государстве плодородные земли были расположены на очень узком участке земли – в долине реки Нил. Каждую весну Нил разливался и удобрял землю плодородным илом. Но при разливе реки смывались границы участков, менялись их площади. Тогда пострадавшие обращались к фараону, он посылал землемеров, чтобы восстановить границы участков, выяснить, как изменилась их площадь и установить размер налога. Восстанавливали границы участков особые чиновники – гарпедонапты — натягиватели верёвок.

Уже у древних греков геометрия означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия. Судя по сохранившимся отрывкам древнеегипетских сочинений, геометрия развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах.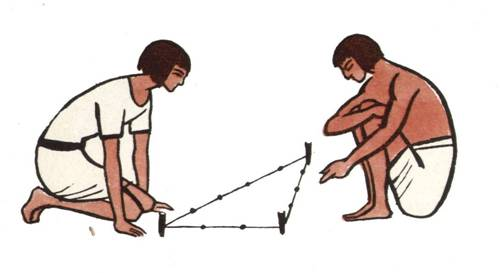

Ремесленникам необходимо было изготавливать посуду, строителям — подбирать камни различной формы для строительства храмов и пирамид, астрономам – измерять углы для определения положения звезд.

Знания постепенно накапливались и систематизировались. Так около

4 тыс. лет назад возникла наука об измерении расстояний, площадей и

объемов, о свойствах различных фигур – геометрия.

Что изучает геометрия?

В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и так далее. Если взять во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.

Происхождение геометрических фигур

Название «фигура» происходит от латинского слова figura, означающего «внешний вид», «образ». Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.

Точка, прямая, плоскость.

А простейшими в геометрии являются три фигуры: — точка, прямая, плоскость. Конечно, самая главная – это точка. Древнегреческий геометр Евклид говорил, что «точка – это то, что не имеет частей». Слово точка по латыни означает результат мгновенного касания, укол. Так, точкой является отверстие, оставленное иглой в листе бумаги. Точка – в русском языке означало конец заточенного гусиного пера. Линия – льняная нить. Луч света также представляет собой модель прямой линии. Натянутая линия – также модель прямой. Плоскость — поверхность.

Все предметы в моем доме напоминают различные геометрические фигуры. Рассмотрим и опишем некоторые из них.

Квадрат

Термин образовался как буквальный перевод соответствующего греческого слова «квадратус» — «четырехугольный».

КВАДРАТ – это прямоугольник, у которого все стороны равны.

Прямоугольник

Термин образован путем соединения двух слов: «прямой» и «угол».

Прямоугольник

— это четырехугольник, у которого все углы прямые.

Треугольник

Треугольник— это многоугольник с тремя сторонами.

Термин образован путем соединения двух слов: «три» и «угол». Слово «три» общеславянское, индоевропейского характера.

Круг

Общеславянское слово, имеющее соответствия в германских языках: в древнегерманском «кригер» — «кольцо», «круг», в греческом — «колесо», «круг»).

Круг— это множество всех точек плоскости, расстояние от каждой из которой до данной точки этой плоскости не больше данного расстояния.

Окружность

В переводе с греческого это слово означает «периферия».

Окружность — это множество точек плоскости, находящихся на данном расстоянии от данной точки, лежащей в той же плоскости и называемой ее центром. Окружность — это граница круга.

Овал

Французское слово «оваль» — «овальный» произошло от латинского «овум» — «яйцо». Овал — замкнутая выпуклая гладкая плоская кривая.

Ромб

Одни считают, что этот термин произошел от греческого слова «ромбос», означающего »бубен», т.к. ромб похож на четырехугольный бубен, другие — что от греческого слова «ромб», которое означает «вращающееся тело», «веретено», т.к. сечение в обмотанном веретене имеет форму ромба.

Трапеция

Греческое слово «трапедзион» переводится как «столик» (сравним со словом «трапеза»). Трапеция — это выпуклый четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны.

Куб

Термин «куб» происходит от греческого слова в переводе означающего — «игральная кость». Она имела форму кубика, и название это перешло на любое тело той же формы. Этот термин впервые встречался у пифагорейцев (VI-IV вв. дон. э.).

Параллелепипед

Термин образован путем соединения двух греческих слов: «параллелос» — «параллельный» и «эпипедос» — «плоскость».

Параллелепипед — призма, основанием котopoй является параллелограмм.

Конус

Конус — от греческого слова «конос» (сосновая шишка, остроконечная верхушка шлема).

Пирамида

Пирамида — от греческого слова «пюрамис», которым греки называли египетские пирамиды. А это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне.

Призма

Призма — от слова «присма» («опиленная», «отпиленная часть»).

Цилиндр

Цилиндр — от латинского слова «цилиндрус» (валик, каток).

Сфера

СФЕРА – латинская форма греческого слова «сфайр» — мяч.

Таким образом, названия геометрических фигур первоначально были названием конкретных предметов, имеющих форму более или менее близкую к форме фигуры.

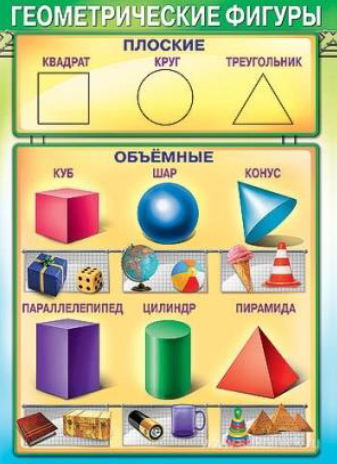
Чем же отличаются плоские и объёмные фигуры?

Плоские можно целиком расположить на одной плоской поверхности.
Объемные фигуры занимают определённое пространство, возвышаются над плоской поверхностью.

Геометрические фигуры в природе

Ученые придерживаются мнения о том, что все, что создается человеком, создается на основе наблюдений за окружающей человека природой. Значит и геометрические фигуры нужно искать в природе. Посмотрите вокруг. Многие окружающие нас предметы напоминают геометрические фигуры.

Вокруг нас находится большое количество предметов, имеющих форму геометрических фигур. Углы, отрезки и плоскости являются объектами искусственного происхождения и изготовлены человеком. Предметы природного происхождения имеют округлые формы, такие как шар, эллипс, дуга. Исключение составляют кристаллы, которые имеют прямоугольные формы.

Дневник наблюдений:

геометрия на кухне

Холодильник

Прямоугольный параллелепипед

Кастрюля

Цилиндр

Тарелка

Круг, окружность

Микроволновая печь

Прямоугольный параллелепипед

Кухонный шкаф

Прямоугольный параллелепипед

Шкаф

Прямоугольный параллелепипед

Кровать

Прямоугольный параллелепипед

Компьютер

Прямоугольник

Стол

Прямоугольник

Банка сгущенки

Цилиндр

Банка молока

Цилиндр

Колбаса

Цилиндр

Сыр

Круг, круговой сектор

Банка йогурта

Усеченный конус

Пачка масла

Прямоугольный параллелепипед

Дом

Прямоугольный параллелепипед

Столб, столбы

Цилиндр, параллельные прямые

Баня

Прямоугольный параллелепипед

Провода электрические

Параллельные прямые

Дорога

Кривая линия

Фонарь

Овал

Морковь

Конус

Бочка

Цилиндр

Теплица

Прямоугольный параллелепипед

Капуста

Шар

Грядка

Прямоугольный параллелепипед

Ведро

Усеченный конус

Лейка

Цилиндр

Крыша

Пирамида, угол

Дом

Прямоугольный параллелепипед

Дверь

Прямоугольник

Окна

Прямоугольник

ЗАКЛЮЧЕНИЕ

Простейшие геометрические фигуры, такие как круг, треугольник, прямоугольник являются именно теми фигурами, с которыми человек познакомился в глубокой древности. Свойства этих фигур первыми пришли на помощь человеку, так как эти фигуры всегда имели широкое применение в практической жизни.

Итак, после проведенной исследовательской работы я могу сделать выводы о наиболее полезных свойствах геометрических фигур:

Окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра.

Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Все движется по кругу.

Треугольник — единственная геометрическая фигура, которая обладает свойством жёсткости. Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей.

Квадрат служит эталоном при измерении площадей всех фигур. Зная о многоугольниках и их видах, можно создать очень красивые предметы украшения, построить разнообразные и уникальные здания.

Человеческие представления о красивом, формируются под влиянием того, что человек видит в живой природе. В различных своих творениях, очень далёких друг от друга, она может использовать одни и те же принципы.

И я могу сказать, что геометрические фигуры создают красоту в искусстве, архитектуре, природе, в окружении человека. Красота – всюду. Есть она и в науке, и в особенности в её жемчужине – математике.

Литература

Клепа. Альманах. №46, 1998г.
Минковский В.Л. За страницами учебника математики. М.: Просвещение, 1966
http://www.kakprosto.ru/kak-807590-kak-voznikla-geometriya#ixzz3ZwNH0Hxi
dic.academic.ru›Геометрия
images.yandex.ru›картинки геометрических фигур
ru.wikipedia.org›Категория:Геометрические фигуры
Математика 6 класс. Учебник для образовательных учреждений. М.: Мнемозина, 2014
Энциклопедия для детей. Математика. Сост. М. Аксенова – М.: Аванта +, 2004
Депман И.Я., Виленкин Н.Я. “За страницами учебника математики” Дрофа 2003
Дорохов А.А., Михайлов М.М., Куценко Г.М., Назаров А.А. “Что такое? Кто такой?” Дрофа 2005

Проект по геометрии «Геометрия вокруг нас»

Геометрия вокруг нас

Проект

1. С геометрией мы встречаемся на каждом шагу, хотя и не обращаем на это внимание. Это наблюдение мне показалось очень интересным, и я решила исследовать тему: «Геометрия вокруг нас».

Цель: научиться узнавать геометрические фигуры в обыденных предметах.

Задачи:

Изучить литературу по данному вопросу.

Завести дневник – таблицу: предмет – фигуры, из которых состоит этот предмет.

Проанализировать и сравнить предметы в жилище, на улице на наличие геометрических фигур.

Нарисовать рисунок с использованием геометрических предметов.

Глава I. Что такое геометрия

1. История возникновения геометрии.

Великий немецкий математик Вильгельм Лейбниц сказал:

«Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет».

Заглянем в прошлое, когда зародилась наука геометрия….

Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.

А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.

Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).

2. Где встречаются геометрические фигуры в нашей жизни.

Некоторые люди, возможно, считают, что различные линии, фигуры, можно встретить только в книгах учёных математиков. Однако, стоит посмотреть вокруг, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Оказывается их очень много. Просто мы их не всегда замечаем. Я решила рассказать, какие геометрические фигуры встречаются вокруг нас.

Глава II. Геометрия вокруг нас

2.1. Геометрия у нас дома.

Все предметы в нашем доме напоминают различные геометрические фигуры. Это видно из дневника наблюдения, который я вела. /Приложение 1/

Рассмотрим и опишем некоторые из них.

Заглянем на кухню. Холодильник, микроволновая печь, газовая плита, кухонный шкаф, стиральная машина имеют форму прямоугольного параллелепипеда. Еще можно эти предметы назвать прямыми призмами, у них все углы между гранями прямые.

Заглянем в холодильник…и что же мы видим, и здесь без геометрии не обошлось. На полках стоят «цилиндры» — банка сгущенки, консервы, кусок колбасы, а сыр напоминает круг.

Кастрюли цилиндрической формы. Ведро, стакан, чайник и лейка похожи на усеченный конус.

Тарелки напоминают круг, край тарелки — окружность.

Крышка стола прямоугольник, я попробовала измерить углы они прямые.

Давайте прогуляемся по спальне. Стены, потолок, окна напоминают прямоугольники .Шкаф, кровать, трельяж, стол – прямоугольные параллелепипеды.

Ковер на полу прямоугольной формы.

Горшки с цветами на подоконниках цилиндрической формы.

Толстая книга похожа на параллелепипед.

Вывод:

В числе всего разнообразия предметов, имеющих сходство, с какими либо геометрическими фигурами у нас дома преобладают отрезки и фигуры прямоугольной формы.

2.2. Геометрия на улице.

Если мы выйдем на улицу, то видим постройки, дома различной геометрической формы. Например дом, баня имеют форму параллелепипеда. Крыши дома – углы.

Столб, бочка для воды имеют форму цилиндра.

Ветки деревьев, электрический столб образуют смежные углы

Фонарные столбы вдоль дороги напоминают отрезки прямой.

А провода можно представить, как параллельные прямые.

В огороде можно тоже встретить геометрию. Грядки как напоказ вычерчены прямоугольники. Морковка уродилась цилиндрической формы, наверно ее и назвали «Цилиндра». Капуста, тыква, арбуз – шар

Заключение

Изучив материал по данной теме, мы выяснили, что геометрия – это древняя наука, раздел математики, которая изучает свойства различных фигур их размеры и взаимное расположение.

В нашей жизни мы часто встречаем геометрические тела и фигуры. Из них состоят все предметы, которые нас окружают, начиная с тарелки с которой едим и заканчивая телевизионной тарелкой, которая передает программы со всего мира.

Дневник наблюдений: Приложение 1

геометрия на кухне

Холодильник

Прямоугольный параллелепипед

Кастрюля

Цилиндр

тарелка

Круг, окружность

Микроволновая печь

Прямоугольный параллелепипед

Кухонный шкаф

Прямоугольный параллелепипед

геометрия в спальне

Шифоньер

Прямоугольный параллелепипед

Кровать

Прямоугольный параллелепипед

Трельяж

Прямоугольный параллелепипед

Стол

Прямоугольник

геометрия в холодильнике

Банка сгущенки

Цилиндр

Банка молока

Цилиндр

Колбаса

Цилиндр

Сыр

Круг, круговой сектор

Банка йогурта

Усеченный конус

геометрия на улице

Дом

Прямоугольный параллелепипед

Столб, столбы

Цилиндр, параллельные прямые

Баня

Прямоугольный параллелепипед

Бочка

Цилиндр

Провода электрические

Параллельные прямые

Дорога

Кривая линия

Фонарь

Овал

геометрия на огороде и в саду

Морковь

Конус

Бочка

Цилиндр

Теплица

Прямоугольный параллелепипед

Капуста

Шар

Грядка

Прямоугольный параллелепипед

Ведро

Усеченный конус

Лейка

Цилиндр

геометрия жилища

Крыша

Пирамида, угол

Дом

Прямоугольный параллелепипед

Дверь

Прямоугольник

Окна

Прямоугольник

Проект по геометрии «Занимательная геометрия».

ГУ «Луговская средняя общеобразовательная школа»

Секция

«Математика, информатика»

Проект

«Занимательная геометрия»

Выполнила: ученица 7 класса

Марченко Милена

Консультант:

учитель математики

Кудайбергенова Гуля Мунтаевна

2015 год

Оглавление

Введение…………………………………………………………… 3

Цели и задачи проекта……………………………………….…… 4

Глава 1. Что такое геометрия……………………………………… 5

1.1История возникновения геометрии…………………………….. 5

1.2.Основные геометрические фигуры……………………… ……9

Глава 2. Геометрия вокруг нас……………………………………. 11

2.1.Геометрия дома……..………………………………………… 11

2.1.Геометрия на улице..…………………………………………… 12

2.1.Геометрия в космосе..………………………………………… ..13

Глава 3. Занимательная геометрия…….…………………………..14

3.1.Задачи со спичками……………………………………………..14

3.2.Пентамино..………………………………………………………14

3.3.Задачи на разрезание…………………………………………….15

3.4.Логические задачи в рисунках………………………………….16

3.5.Геометрия в стихах………………………………………………16

Заключение…………………………………………………………..16

Литература……………………………………………………………17

Введение

Мир, в котором мы живем, наполнен геометрией – геометрией домов и улиц, гор и полей, творениями природы и человека. Все, что мы видим вокруг (прямоугольник окна, загадочный узор снежинки, дома-параллелепипеды, капля воды, велосипедная шина), так или иначе относится к геометрии. О происхождении геометрии, об использовании геометрических знаний на практике, о занимательных и интересных задачах и о многом другом я расскажу в своем проекте.

Актуальность

На уроках математики мы изучали прямоугольный параллелепипед и я узнала, что это геометрическая фигура. Ведь про треугольник, прямоугольник, окружность, квадрат говорят тоже геометрические фигуры. А что же это за наука геометрия? Что же она изучает?

Мы семиклассники стоим в начале пути в мир геометрии. На самом деле этот мир окружает нас с самого рождения. Ведь, все что мы видим вокруг: прямоугольник окна, загадочный узор снежинки, дома-параллелепипеды, капля воды, узел веревки. Так или иначе, все относится к геометрии, ничто не ускользает от её внимательного взгляда. Хочется, как можно больше узнать о геометрии. С помощью свойств геометрических фигур научиться видеть красоту обычных вещей, смотреть и видеть, думать и делать выводы.
И прекрасный мир геометрии постепенно пойдет нам на встречу, начнет открывать свои тайны.

В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».
С геометрией мы встречаемся на каждом шагу, хотя и не обращаем на это внимание. Это наблюдение мне показалось очень интересным, и я решила исследовать тему: «Занимательная геометрия».

Проблема

В учебниках по геометрии все написано математическим языком, но в большинстве случаев он малопонятен и малоинтересен учащемуся с небольшим багажом математических знаний.

Цели и задачи проекта

Поэтому, я хотела бы в своей работе: доступнее преподнести материал, используя такие средства, как различную литературу, сайты Интернета поисковые системы: Yandex, Rambler, Google, собственные задумки и предложения, электронную презентацию.

Основная цель работы состоит в том, чтобы показать, как интересна и занимательна геометрия вокруг нас.

Методы и приёмы работы над проектом

Основной метод, который я использую в своей работе,- это метод систематизации и обработки данных. Привлекая информационные технологии, я хотела бы разнообразить материал, привлекая внимание моих сверстников.

Ожидаемый результат

Практическое применение моей работы состоит в том, чтобы помочь моему учителю математики, и учителям математики и физики других школ преподнести этот материал интересно и красочно.

Особенности проекта

Этот проект доказывает, что проектная деятельность по математике невозможна без использования ИКТ.

Глава 1. Что такое геометрия?

1.1.История возникновения геометрии.

Великий немецкий математик Вильгельм Лейбниц сказал: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет».

Откуда пошла геометрия.
Геометрия… откуда взялось это слово? Что оно означает? Попробуем разгадать его смысл. «Гео» означает «Земля», «метр» — это единица измерения длины (от греческого слова «метрео» — «измеряю». Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».

Какова же история ее возникновения?
Такой вопрос задавали еще в Древней Греции и отвечали на него так: «Геометрия была открыта египтянами и возникла при измерении земли. Нет ничего удивительного в том, что эта наука как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного состояния переходит в совершенное. Зарождаясь путем чувственного восприятия, оно постепенно становится предметом рассмотрения и наконец, делается достоянием разума». Эти замечательные слова приписывают греческому ученому Евдему Родосскому, жившему в IV в.до н.э.
В «Энциклопедическом словаре юного математика» написано: «Геометрия – одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках».

Перевозить грузы на катках было довольно тяжело потому, что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки и с их помощью перетаскивать грузы. Так появилось первое колесо.
Но не только в процессе работы знакомились люди с геометрическими фигурами. Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).

Для того чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы. Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д. Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов.
Египетские пирамиды насчитывают 4800 лет, а их строительство, очевидно, требовало достаточно точных геометрических расчетов, так как состоят они из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
«Все боится времени, но само время боится пирамид».

В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра. Без математических знаний все эти сооружения невозможно было бы построить.

Но особо важной была задача распределения земельных участков. В Египте плодородная земля тянется узкой полоской в долине Нила, а за ее пределами простирается пустыня. Поэтому каждый ее клочок представлял большую ценность. Ежегодно разливы Нила смывали границы участков, нужно было восстанавливать их как можно точнее. Этим занимались специальные землемеры, которые и были, можно сказать, первыми геометрами.

И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.
Если в Древнем Египте геометрия была сугубо прикладной наукой, то в древней Греции она стала математической теорией. И имена знаменитых греков будут постоянно встречаться нам в курсе геометрии.

Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз Академии Платона гласил: «Да не войдёт сюда не знающий геометрии».

Настает время привести все разрозненные знания в систему.
Евклид жил в Александрии около 300 года до нашей эры, был современником царя Птолемея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии, придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.

Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.
В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах. Ученый гордо ответил: » В геометрии нет царской дороги».

В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида.
Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией».

Различные математические открытия определили следующие направления в математике.

Сделаем вывод геометрия – это древняя наука, раздел математики, которая изучает свойства различных фигур их размеры и взаимное расположение.

Разнообразие формы и цвета
Нам подарила родная планета.
А геометрия — это
Наука о форме предмета.

1.2. Основные геометрические фигуры

Изучением геометрических фигур занимаются различные разделы геометрии.

Геометрические фигуры, точки которых лежат в одной плоскости, изучает планиметрия.

ТОЧКА, одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.

ПРЯМАЯ, одно из основных понятий геометрии. Можно провести через любые две точки и притом одну.

ОКРУЖНОСТЬ, замкнутая плоская кривая, все точки которой одинаково удалены от ее центра O.

ПРЯМОУГОЛЬНИК, четырёхугольник, у которого все углы прямые.

КВАДРАТ, равносторонний прямоугольник.

КРУГ, часть плоскости ограниченная окружностью.

ТРАПЕЦИЯ, четырехугольник, у которого две стороны параллельны, а две другие нет.

ПАРАЛЛЕЛОГРАММ, четырехугольник у которого противоположные стороны попарно параллельны.

РОМБ, параллелограмм у которого все стороны равны.

ПАРАЛЛЕЛЕПИПЕД, призма, основанием которой служит параллелограмм. «Призма» — латинская форма греческого слова «присма» — опиленная (имелось в виду опиленное бревно)

КОНУС, геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов. «Конус» — латинская форма греческого слова «Конос», означающего сосновую шишку.

ЦИЛИНДР, геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. Означает «валик», «каток».

ПИРАМИДА, многогранник, основание которого представляет собой многоугольник, а остальные грани — треугольники с общей вершиной. Это название пошло от египетских пирамид.

ШАР, часть пространства ограниченного сферой.

Глава 2. Геометрия вокруг нас.

2.1. Геометрия у нас дома.

Рассмотрим и опишем некоторые из них.

Заглянем на кухню. Холодильник, микроволновая печь, газовая плита, кухонный шкаф, стиральная машина имеют форму прямоугольного параллелепипеда. Потому что, как и у параллелепипеда все противолежащие грани прямоугольники их всего 6, 12 ребер, 8 вершин, есть три измерения – длина, ширина, высота. Еще можно эти предметы назвать прямыми призмами, у них все углы между гранями прямые.

А чайник похож на усеченный конус. Дно чайника круг, а крышку откроем, увидим еще одну окружность только меньшего размера.

Лейка похожа на конус.

Кастрюли цилиндрической формы. И действительно – у них имеется два круга, лежащие в параллельных плоскостях и стенка, которую можно представить как множество отрезков, соединяющих соответствующие точки на этих кругах.

Тарелки напоминают круг, край тарелки – окружность. Крышка стола прямоугольник, я попробовала измерить углы они прямые.

Давайте заглянем вовнутрь холодильника и что же мы видим, и здесь без геометрии не обошлось. На полках стоят «цилиндры» — банка сгущенки, банка молока, консервы, кусок колбасы, а сыр напоминает круг.

Прогуляемся по спальне. Шкаф, кровать, трельяж, стол – прямоугольные параллелепипеды. Ковер на полу прямоугольной формы. Горшки с цветами на подоконниках цилиндрической формы. Абажур формой конуса.

Толстая книга похожа на параллелепипед. Двери имеют форму прямоугольников. Стены, потолок, окна так же напоминают прямоугольники.

Вывод:

2.2. Геометрия на улице.

Если мы выйдем на улицу, то видим постройки, дома различной геометрической формы. Например, дом, баня имеют форму параллелепипеда. Крыши дома – углы. Столб, бочка для воды имеют форму цилиндра.

На улице мы видим предметы, изготовленные человеком и предметы природного происхождения. Например: жилой дом, построенный человеком. Это параллелепипед.

Фонарные столбы вдоль дороги напоминают отрезки прямой.

Крыша трансформаторной подстанции это треугольная призма. У неё есть две треугольные стороны, лежащие в параллельных плоскостях и боковые поверхности, которые и образуют призму.

А провода можно представить, как параллельные прямые.

Объект природного происхождения — русло реки. Его можно представить как кривую линию.

2.3. Геометрия в космосе.

Поиск геометрических фигур в предметах, которые нас окружают, был бы не полным, если бы мы не обратились к космическим объектам и не определили, форму каких фигур они имеют. Рассмотрим форму планет, звёзд, галактик и траектории их движения в пространстве.

Планеты:

Имеют шарообразную форму. Доказано, что все планеты солнечной системы своей формой напоминают шар.

Звёзды:

Являясь космическими объектами, звёзды, так же как и планеты имеют форму шара. Солнце напоминает огромный шар.

Галактики:

Учёные установили, что галактики очень часто имеют форму геометрической фигуры, которая называется спираль.

Орбиты планет:

Планеты движутся вокруг солнца по траекториям, имеющим форму эллипса. Известно, что смена времён года на Земле происходит именно потому, что орбита Земли – эллипс.

Вывод: в космическом пространстве находятся объекты только круглой или другой криволинейной формы и отсутствуют прямолинейные объекты.

Глава 3. Занимательная геометрия.

3.1.Задачи со спичками.

Головоломки со спичками уже давно используются в качестве задач для развития логики и творческого мышления. Популярность подобных заданий обусловлена удобством использования и доступностью материала, из которого составляются занимательные геометрические фигуры. Разгадывать такие головоломки можно дома, на работе, на улице или в дороге: достаточно найти ровную поверхность для выкладывания нужных схем из спичек. Логические задачи на перекладывание спичек бывают как простыми и сложными, поэтому они подходят как для детей младших классов (несмотря на то, что «спички детям не игрушка»), так и для взрослых. Я собрала интересные задачи со спичками различного уровня сложности. /Приложение 2/

3.2.Пентамино.

“Пентамино” — одна из самых популярных мировых головоломок, пик популярности пришелся на конец 60-х годов. В эту головоломку могут играть и дети и взрослые.

Запатентовал головоломку “Pentomino” Соломон Вольф Голомб, житель Балтимора, математик и инженер, профессор университета Южная Калифорния. Игра состоит из плоских фигур, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами, отсюда и название. Существуют еще версия головоломок Тетрамино, состоящие из четырех квадратов, от этой игры и произошел известный Тетрис.

Элементы Пентамино

Игровой набор “Пентамино” состоит из 12 фигурок. Каждая фигура обозначается латинской буквой, форму которой она напоминает. При решении задач и головоломок фигурки можно вертеть и переворачивать. /Приложение 3/

3.3.Задачи на разрезание.

Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих простых задач на разрезание были найдены еще древними греками, китайцами, но первый систематический трактат на эту тему принадлежит перу Абул-Вефа, знаменитого персидского астронома Х века, жившего в Багдаде. Геометры всерьез занялись решением задач на разрезание фигур на наименьшее число частей и последующее составление из них той или иной новой фигуры лишь в начале XX века. Одним из основоположников этого увлекательного раздела геометрии был знаменитый составитель головоломок Генри Э. Дьюдени. Особенно большое число существовавших ранее рекордов по разрезанию фигур побил эксперт австралийского патентного бюро Гарри Линдгрен. Он является ведущим специалистом в области разрезания фигур.

В наши дни любители головоломок увлекаются решением задач на разрезание прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берется за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению. Поскольку здесь не требуется глубокое знание геометрии, то любители иногда могут даже превзойти профессионалов-математиков.

Вместе с тем, задачи на разрезание не являются несерьезными или бесполезными, они не так уж и далеки от серьезных математических задач. Из задач на разрезание родилась теорема Бойаи–Гервина о том, что любые два равновеликих многоугольника равносоставлены (обратное очевидно), а затем и третья проблема Гильберта: верно ли аналогичное утверждение для многогранников?

Задачи на разрезание помогают как можно раньше формировать

геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе. /Приложение 4/

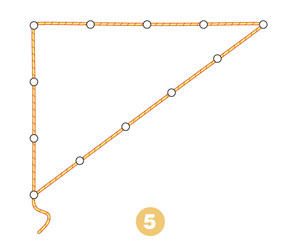
3.4.Задачи в рисунках.

Задачи в рисунках очень нравятся учащимся. Такие задачи очень интересны и занимательны. /Приложение 5/

3.5.Геометрия в стихах.

Для доступности понятий по геометрии учащимся можно воспользоваться геометрией в стихах. Это намного легче и интереснее. /Приложение 6/

Заключение

Я считаю, что презентация, которая получилась в результате проекта содержательная, занимательная и красочная, что позволит, посмотревшим её людям, ознакомится с геометрией в доступной интересной форме. Работа потребовала от меня большой усидчивости, терпения и времени. Но я не буду останавливаться на достигнутом. Планирую в дальнейшем расширить свою работу, пополняя её новыми знаниями по геометрии, надеясь, что моя работа стоит моих усилий!

Литература

1. Ф. Рудио, О квадратуре круга, ГТТИ, 1934

2. В. П. Щереметевский, Очерки по истории математики, Учпедгиз, 1940

3. С. Я. Лурье, Архимед, АН СССР, 1945

4. С. Н. Шрейдер, Три задачи древней геометрии. Из опыта проведения внеклассной работы по математике в средней школе, Учпедгиз, 1955

5. В. И. Лебедев, Очерки по истории точных наук, вып. 4, Знаменитые задачи древности, М., 1917

6. Электронные ресурсы:

http://www.igelnik.ru

http://www.b-i-o-n.ru

Научно-практическая работа «Геометрия в нашей жизни»

Городская научно-практическая конференция школьников «Первые шаги в науку»

Возрастная категория: «Юниор»

Секция: математика

Название работы:

«Геометрия в нашей жизни»

Автор работы:

Кузнецов Григорий Андреевич

г.о.Тольятти, МБУ «Школа №25», 5 класс

Научный руководитель:

Кофанова Ирина Анатольевна,

учитель математики МБУ «Школа №25»

г.Тольятти

2017

Содержание

Введение

Основное содержание

1. История геометрии

2. Геометрия вокруг нас

3. Полезная геометрия

4. Геометрия в моем доме

Выводы

Список использованных источников и литературы

Приложение

Многие думают, что геометрия – сложная, скучная, бесполезная и далекая от реальной жизни наука и поэтому удивляются, узнав, что она появилась из-за необходимости решать практические задачи.

Ученики обычно думают, что математика не имеет практического применения. А ведь геометрия, один из основных разделов математики, тесно связана с нашей повседневной жизнью. Наши дома полны объектов, созданных с использованием точных геометрических форм, хотя мы можем этого и не осознавать. Нельзя начертить ни один чертеж, будучи незнакомым с этой древней наукой, нельзя определить количество рулонов обоев не зная площади комнаты, нельзя построить ни одно техническое или архитектурное сооружение без этой науки, даже в создании ландшафта просто никак без неё не обойтись. Вот и получается, что геометрия – это всё же та наука, пренебрегать которой нельзя и в своей работе я постараюсь это показать.

Мы с родителями решили сделать ремонт в моей комнате. И я на примере своей семьи решил показать, как важно знать азы геометрии.

Тема моей работы: Геометрия в нашей жизни.

Цель: Доказать и на примере своей семьи показать, что геометрия очень важна в нашей жизни.

Задачи:

Узнать больше о науке геометрии.
Определить связь между геометрией и нашей жизнью.
Составить смету ремонта моей комнаты.

Используемые методы: Изучение литературы и интернет-источников по данной теме, анализ и обобщение полученной информации, практическая работа.

Практическая ценность работы: Данную работу могут использовать учителя при изучении темы «Начальные сведения о геометрии»; работа является подготовительным этапом ремонта моей комнаты.

Основная часть

1. История геометрии

Возникновение геометрии уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельности человека и наблюдением за окружающим миром.

Слово «геометрия» греческое и в переводе на русский язык означает «землемерие». Исторические памятники и археологические находки свидетельствуют о том, что задолго до нашей эры в древнем Вавилоне и Египте люди владели некоторыми геометрическими знаниями. Для решения задач, связанных с земледелием и строительством, требовались умения измерять величины (длину, площадь, объем и другие), знания законов геометрических построений и расчетов. Одно из чудес света — египетские пирамиды свидетельствуют о достижениях египтян в области геометрии.

Греки заимствовали накопленные сведения о геометрических фигурах и применяли их, например, при измерении земельных участков. Они же и придумали название науке, которое используется до сих пор во всех странах мира: «геос» -земля, «метрио» — измеряю. Геометрия, возникшая из практических потребностей человека, постепенно становилась теоретической наукой. Появились ученые, объектами изучения которых стали не только бытовые задачи, а непосредственно геометрические фигуры и их свойства: Фалес (624-547 до н.э.), Пифагор (580-496 до н.э.), Платон (429-348 до н.э.), Евклид (III в. до н.э.) и другие.

Основной заслугой Евклида является создание «Начал» — самого распространенного научного сочинения в мире. В 13 книгах им были систематизированы все предыдущие знания геометрии и арифметики. По «Началам» Евклида многие поколения людей на протяжении двух с лишним тысячелетий изучали геометрию, которая получила название евклидовой геометрии.

Переворот в геометрии произошел в начале XIX в. Некоторые ученые пришли к мысли о создании геометрии, отличной от евклидовой. Великому русскому математику Н.И.Лобачевскому ( 1792-1827) было 34 года, когда он построил свою неевклидову геометрию. Прошло время, и ученые стали выводить геометрические формулы, теоремы, аксиомы, сформулировалось понятие, что изучает геометрия.

2. Геометрия вокруг нас

Геометрические знания широко применяются в жизни. Геометрия встречается очень часто в строительстве, ландшафтном дизайне, архитектуре и интерьере. И это далеко не все отрасли.

Развитие цивилизации повлекло за собой развитие науки. Геометрией занимались многие ученые, и в результате их научных работ, геометрия нашла себе место на практики. О том, для чего нужна геометрия, можно рассказывать очень много. В первую очередь она связана с такими науками, как инженерия, физика, астрономия, что дает возможность проводить новые открытия и разрабатывать перспективные проекты. Все инженерные расчеты связаны с геометрией, даже, казалось бы, такие мелочные, как, например, установка уличных фонарей. Ведь для этого нужно с высокой точностью просчитать угол падения луча света на землю, чтобы он смог максимально осветить территорию. Также геометрия нужна перед началом строительства. Архитекторы должны с точностью рассчитать все моменты строительства. Законам геометрии подчиняются траектории и габариты транспорта, поэтому водители должны учитывать это для безопасного движения. Можно приводить еще много примеров из жизни, где геометрия занимает не последнюю роль. Рассмотрим некоторые из них.

Геометрия в архитектуре

Городское пространство – это мир геометрических тел. Повсюду возвышаются статные призмы. Архитектурные здания в большинстве своём – многогранники, а также их простые и сложные комбинации. И это не тенденция современности. Так было испокон веков. Геометрия и потребности человека в комфорте, красоте и самовыражении диктуют свои правила. Прочность, красоту и гармонию зданий во все времена обеспечивала геометрия.

Прямые призмы – самые распространённые многогранники в архитектуре любого города. Это маленькие «хрущевки», многоэтажные дома, а также массивные небоскрёбы. Характерным примером прямой призмы может стать известная на весь мир шестигранная башня Пирелли, возведённая в Милане в 1960 году.

В Мадриде располагается еще один не менее примечательный архитектурный объект. Башни «Ворота в Европу», имеющие форму наклонных призм, собирают вокруг себя не меньше туристов, чем здание Пирелли.

Зданиям-призмам конкуренцию составляют архитектурные объекты в форме правильных пирамид, правда, не по количеству, а по популярности.

Здание Национальной библиотеки Белоруссии по праву заслужила статус одного из самых оригинальных строений мира из-за своей формы ромбокубооктаэдра. Это архимедово тело состоит из 18 квадратов и 8 треугольников. Из-за такой формы библиотеку нередко сравнивают с алмазом или бриллиантом.

Городской пейзаж требует постоянных изменений, поэтому применение многогранников в архитектуре приобретает в последнее время несколько иной характер. Архитекторы-новаторы ломают стереотипное представление о красоте зданий, используя в своих проектах теперь уже невыпуклые геометрические тела.

Геометрия и архитектура непосредственно связаны – геометрия является незаменимой частью архитектуры, одной из ее основ.

Геометрия в живописи

Геометрия является связующим стержнем, который проходит через всю историю живописи.
В самом деле, существуют три принципиальных геометрических метода отображения трёхмерного пространства на двумерную плоскость картины: метод ортогональных проекций, аксонометрия и перспектива.
Существует техника геометрической живописи, которая является одной из ранних этапов развития искусства Древней Греции (IX-VIII вв. до н. э.). Это проявляется в росписи утвари. Геометрическому стилю присуще многообразие и четкость узоров, их строгость подчёркивает построение конструктивного предмета . Орнамент располагается полосами и получается из ломанных линий, крестов, окружностей. В более поздний период развития Древней Греции появляется изображение образа человека из геометрических фигур.

В творениях художников присутствует геометрия.

Геометрия в природе

Очень част в природе мы сталкиваемся с геометрией. Фигура, близкая с кругу, получится, если разрезать поперек апельсин или арбуз, блин тоже напоминает нам круг. Дугу можно увидеть на небе после дождя — это радуга.

В детстве мы любили играть с мыльными пузырями, эти тела имеют сферическую поверхность. Некоторые деревья, одуванчики, отдельные виды кактусов также имеют сферическую форму. Многие ягоды имеют форму шара, например крыжовник, смородина, черника. Шаровую форму принимают капельки росы, капли ртути из разбитого градусника, капли масла, оказавшиеся в толще воды. Все жидкости в состоянии невесомости обретают форму шара.

Необыкновенно красивы и разнообразны многогранники, созданные природой.

Кристалл соли имеет форму куба. Алмазы чаще всего встречаются в виде октаэдра, иногда куба. Существуют и многие микроскопические многогранники. В микроскоп можно увидеть, что молекулы воды при замерзании располагаются в вершинах и центрах тетраэдров. Атом углерода всегда соединен с четырьмя другими атомами тоже в форме тетраэдра.

В творениях природы тоже присутствует геометрия.

Геометрия в одежде

Геометрия вдохновляла и продолжает вдохновлять дизайнеров. Геометрия является основоположницей моды. С помощью геометрии, с помощью знаний о подобии, о пропорциях, геометрических фигур люди могут создавать не только удобную одежду, но и придавать ей колоритность, выделять из серой массы, делать ее модной и красивой. Без геометрии не обойдется ни один чертеж, ни одна выкройка, так необходимая для создания модной и удобной одежды. Дизайнеры применяют геометрические фигуры для создания силуэта, в принте тканей, используют их, чтобы разнообразить образ аксессуарами.

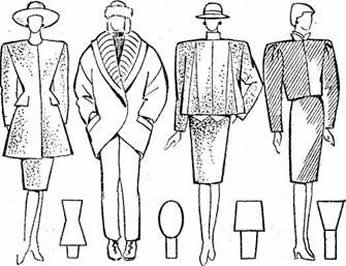
Роль геометрии в моде огромна. Благодаря ей, в нашем гардеробе столько нарядов с рисунком в полоску, клетку, в елочку, в горошек и т. д.

3. Полезная геометрия

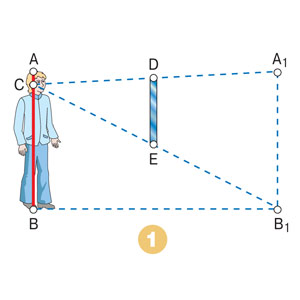
Вешаем зеркало

Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота от нижнего края зеркала до пола должна быть вдвое меньше расстояния от пола до глаз. На каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нем с головы до ног.

Завариваем чай

Время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника.

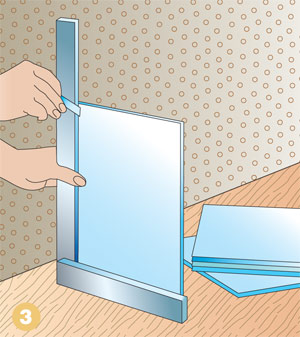
Выдерживаем прямые углы

Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строительный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину.

Строим прямой угол на земле

Известен старинный способ построения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка. В таком треугольнике один из углов получается прямым.

Проверяем перпендикулярность стен

Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы. Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный треугольник со сторонами 3, 4, 5 — прямоугольный.

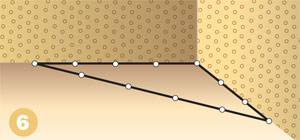
Отмеряем нужный объем

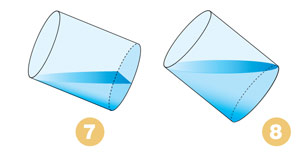
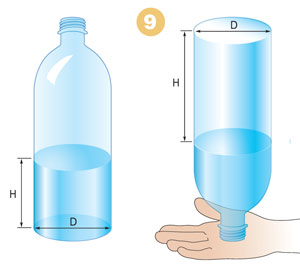
Воспользуемся стаканом цилиндрической формы. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). Чтобы узнать объем бутылки, надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объем бутылки равен сумме найденных объемов.

Укрепляем калитку

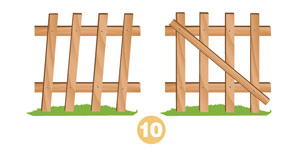
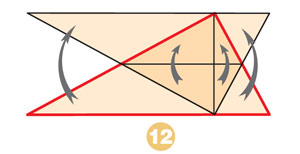
Прямоугольная калитка со временем расшатывается и становится похожей на параллелограмм. Этого можно избежать, прибив к ней еще одну планку. Выбор такого положения планки основан на свойстве жесткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

Выбираем табурет

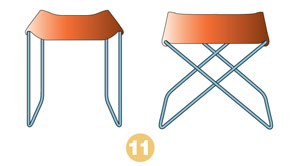
Безопасный табурет изображен справа, так как его сиденье и ножки образуют треугольник.

Исправляем ошибку кроя

Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Для исправления ошибки вы можете разрезать один из треугольников, а затем сложить из него нужный треугольник.

4. Геометрия в моем доме

Мои родители давно подумывают о ремонте моей комнаты. Я решил поторопить их и провести всю подготовительную работу. Чтобы подготовиться к ремонту, мне предстояло измерить площади потолка, пола и стен, периметр моей комнаты; выбрать отделочный материал, произвести расчеты его количества и стоимости, а так же стоимости отделочных и монтажных работ. И вот, что у меня получилось.

1) Выбираю потолок, рассчитываю стоимость:

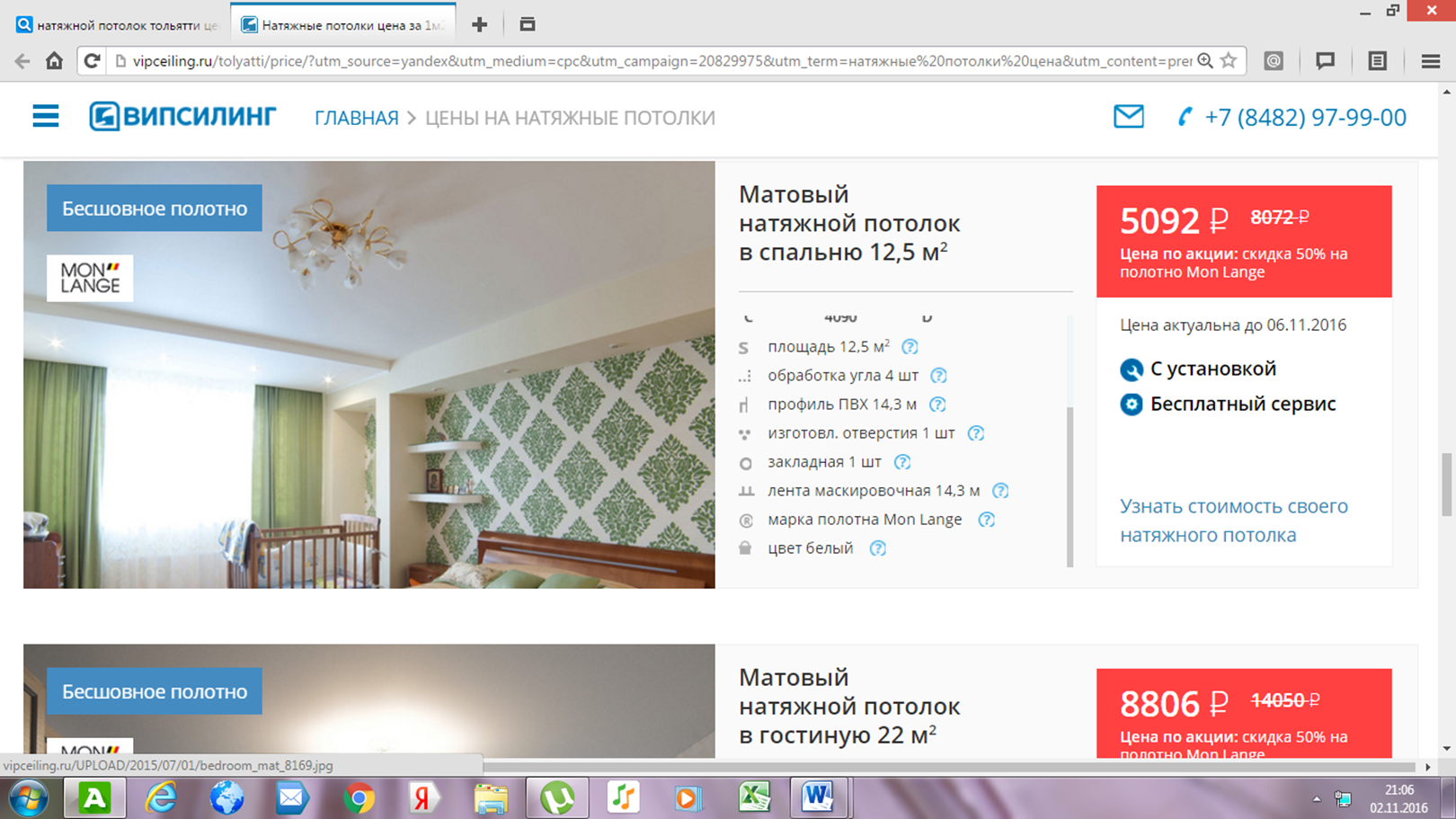
Площадь потолка в моей комнате — 12,2 м²

5092 : 12,5 = 407,79 р.

407 36 *12,2 = 4969,79 р.

Если же скидки на момент ремонта не будет, то стоимость составит:

8072 : 12,5 = 661,63 р.

661,63 * 12,2 = 8071,88 р.

Итого: 4969,79 р. или 8071,88 р. (без скидки)

2) Выбираю пол, рассчитываю стоимость:

Площадь пола – 12,2 м²

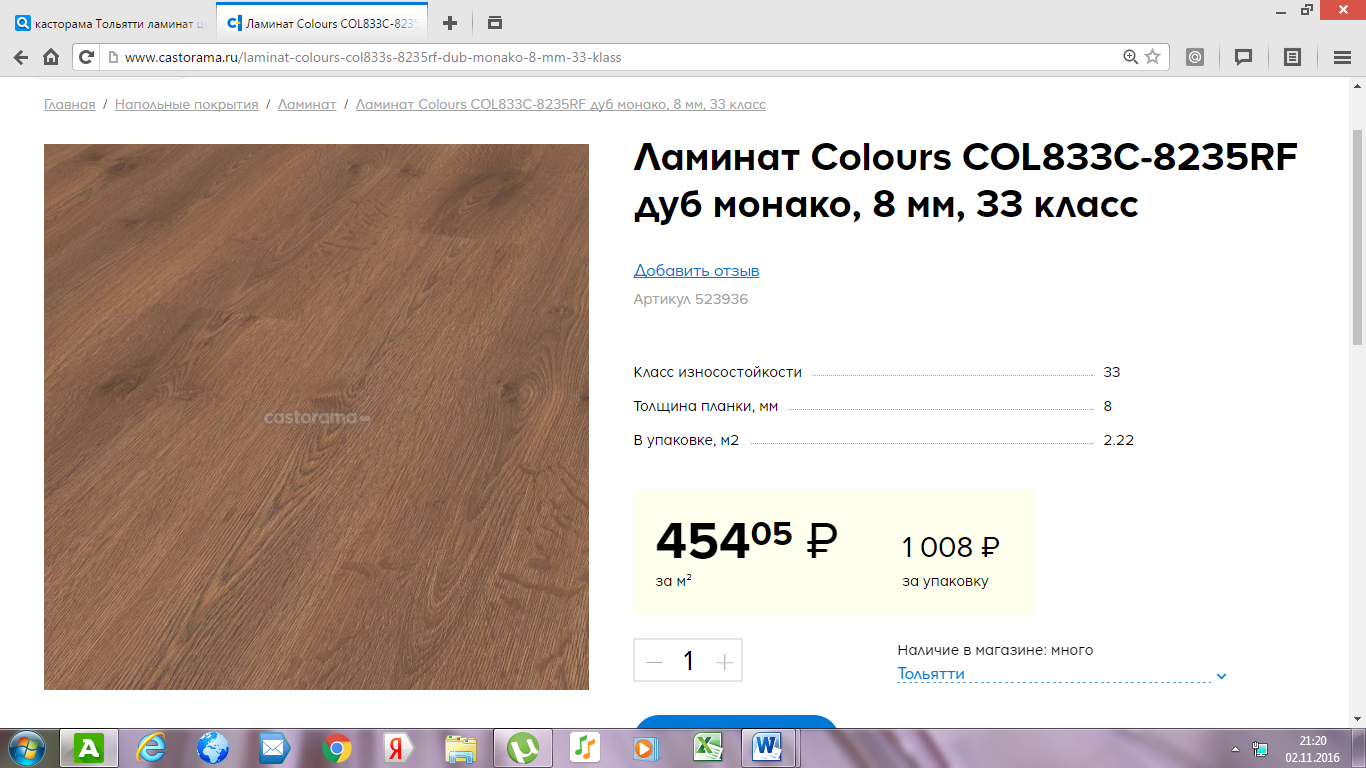
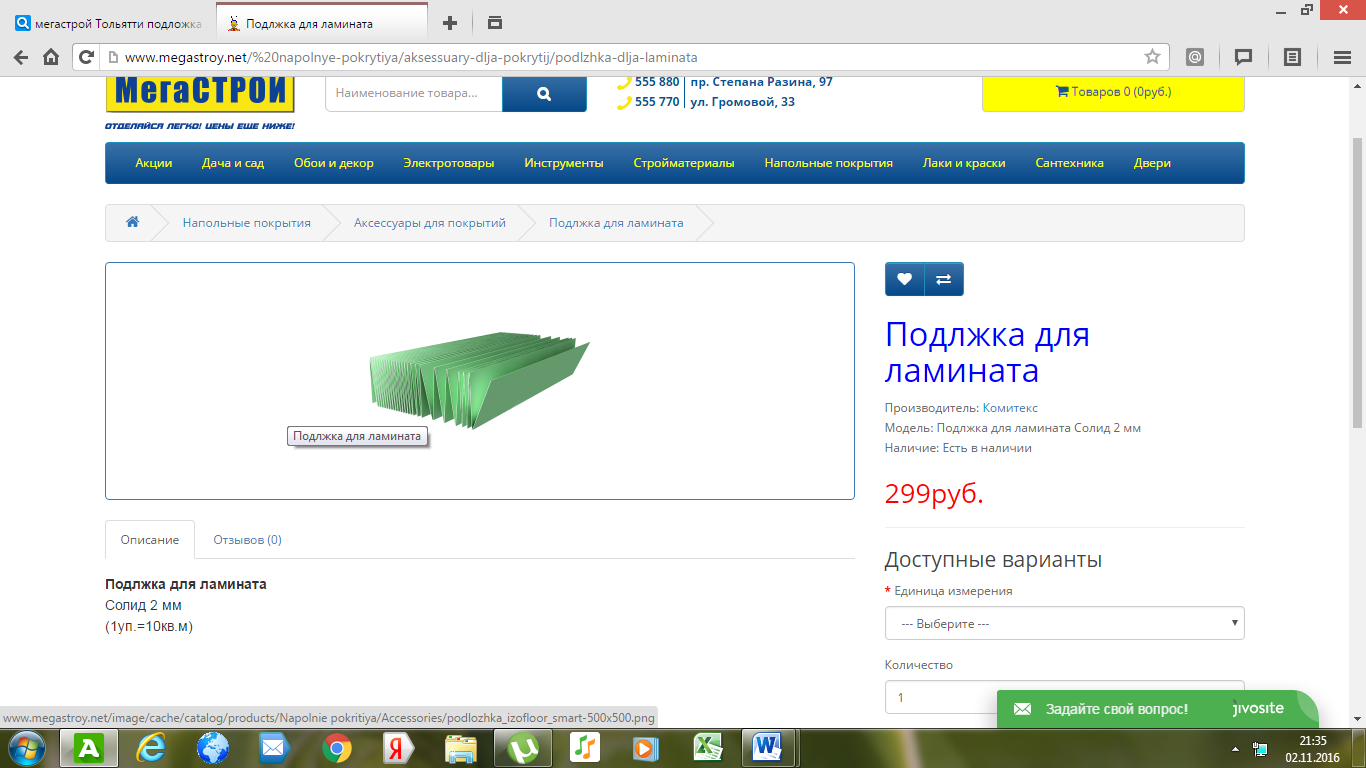
1. Ламинат: 454,05*12,2 = 5539,41 р.

2. Укладка ламината: 300р./м², 300*12,2=3660 р.

3. Подложка для ламината: 299*2 = 598 р.

4. Плинтус: понадобится 11,53м, 49*11,53 = 564,97 р.

5. Монтаж плинтуса: 120р./м, 120*11,53 = 1383,6 р.

Итого: 11745,98 р.

3) Выбираю отделку стен, рассчитываю стоимость:

Общая площадь стен за вычетом двери, окна и встроенного шкафа-купе — 27,42м²

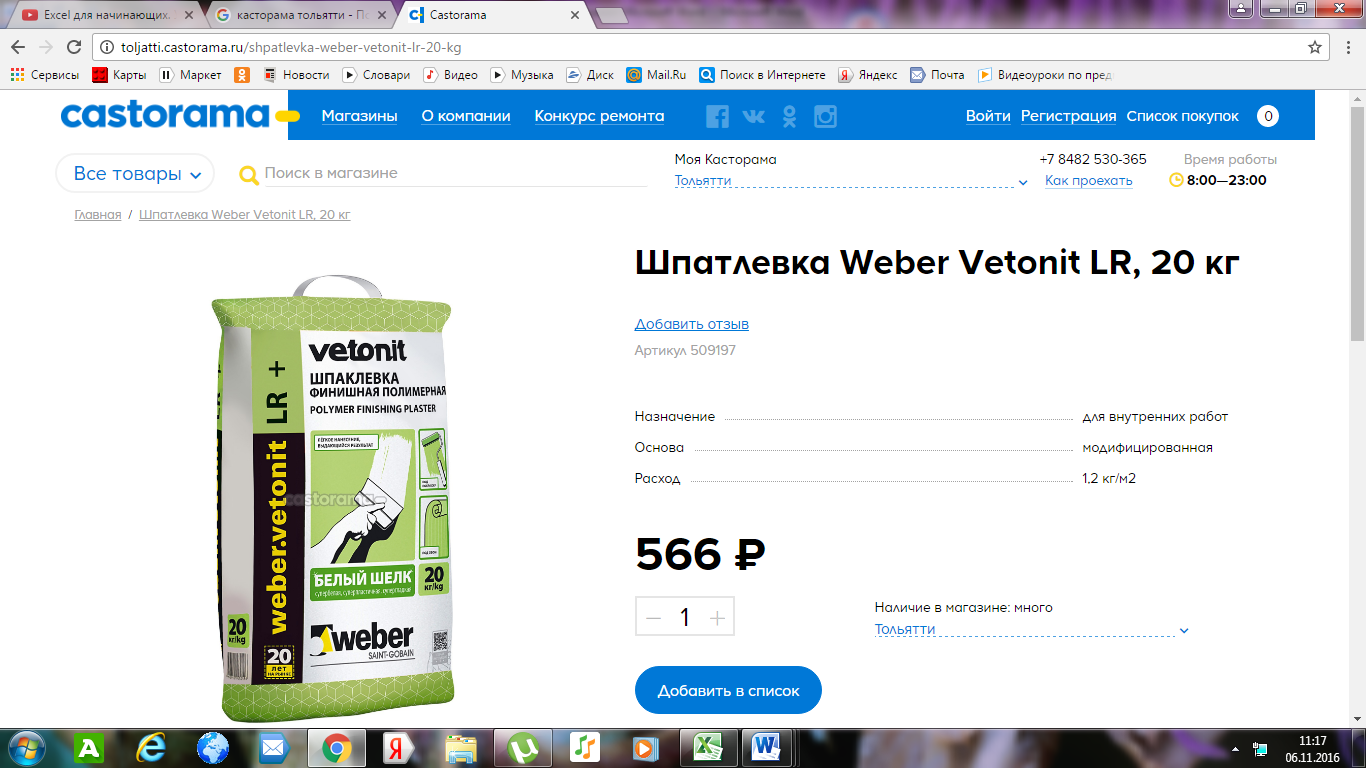
1. Шпатлевка: расход на 1 м² — 1,2 кг, мешка 20 кг не хватит, нужно купить еще мешок 5 кг. 566 + 293 = 859 р.

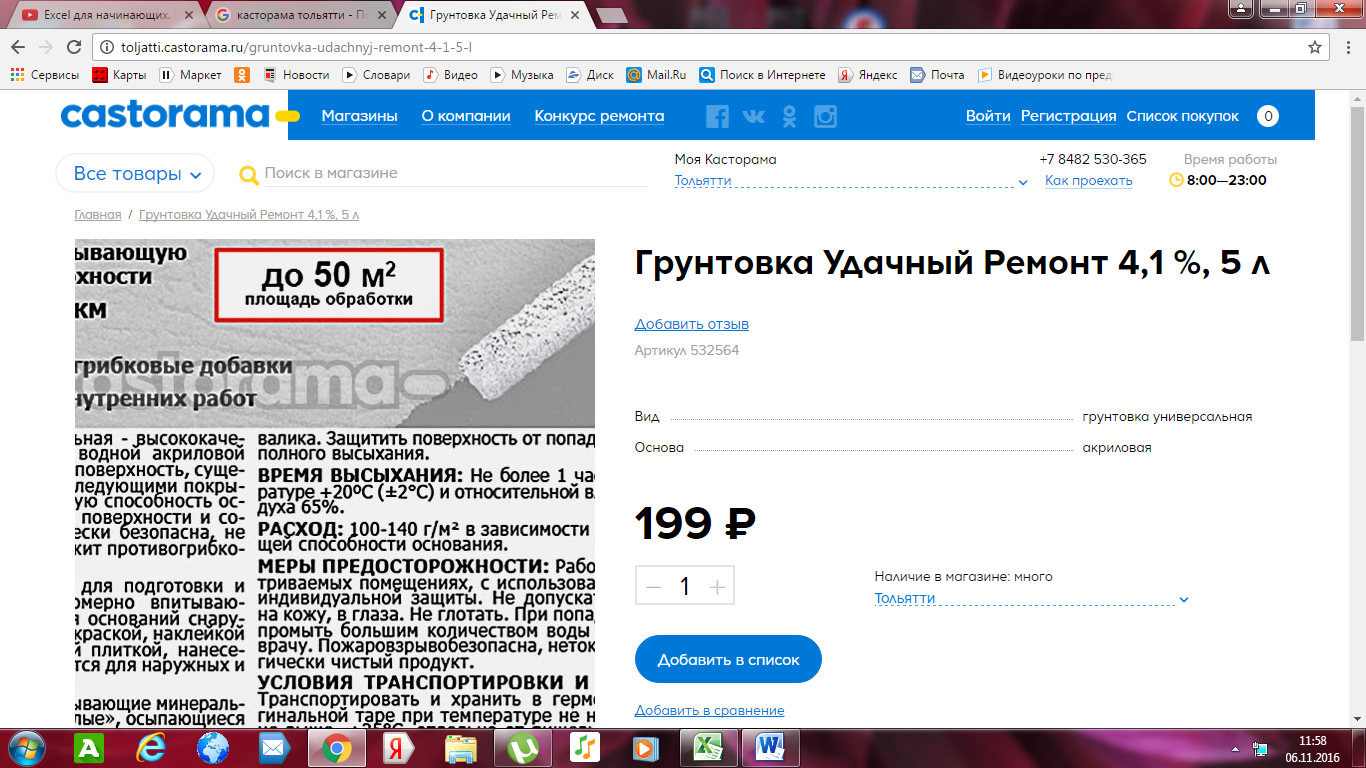
2. Грунтовка «Удачный ремонт»: хватает для обработки площади до 50м², 199 р.

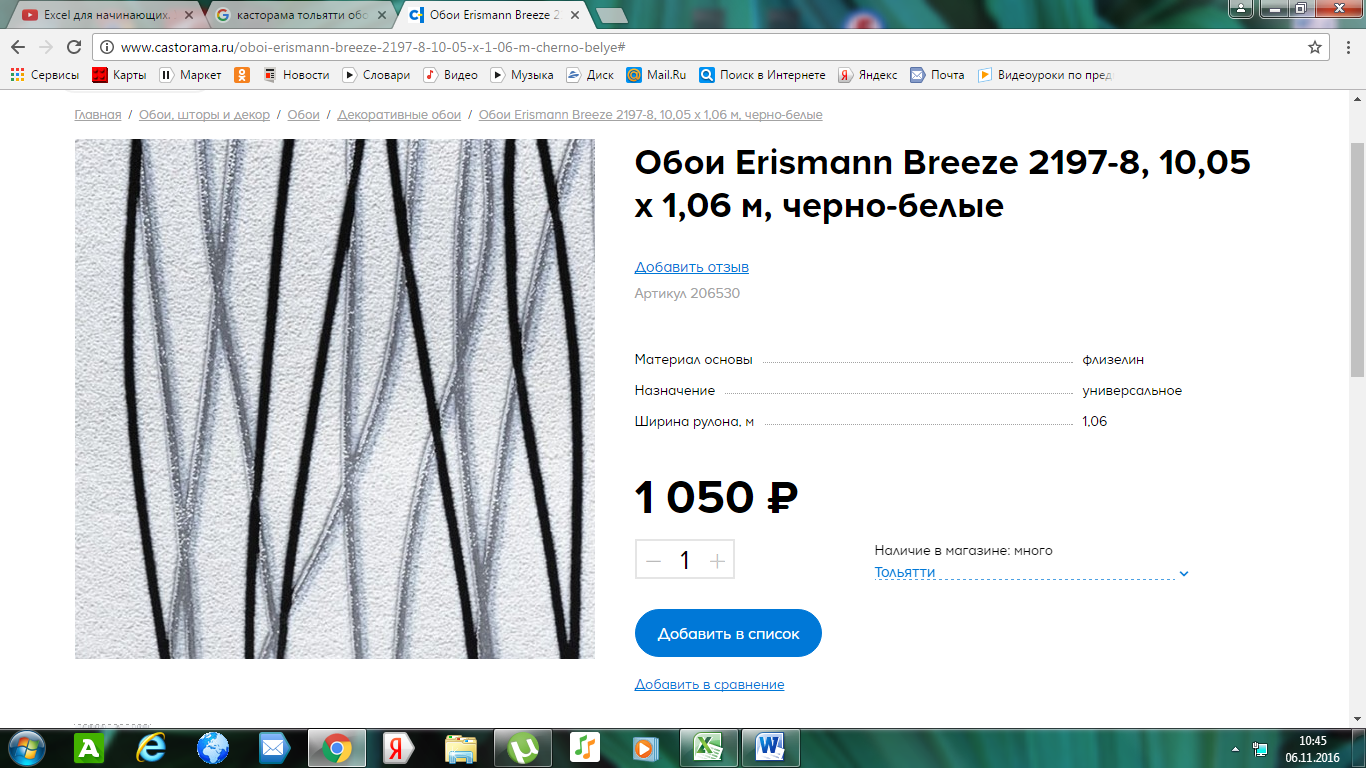
3. Обои: Рулона обоев хватит, чтобы оклеить 1,06*10,05 = 10,65м². Понадобится 3 рулона таких обоев. 1050*3 = 3150 р.

4. Ремонтные работы:

Шпатлевка стен — 150р./м² 150*27,42 = 4113 р.

Грунтовка стен — 25 р./м² 25*27,42 = 685,5 р.

Наклейка обоев — 100 р./м² 100*27,42 = 2742 р.

Итого: 11748,5 р.

Итак:

Потолок — 8071,88 р.

Пол — 11745,98 р.

Стены — 11748,5 р.

Итого на ремонт: 31566,36 р.

Выводы

Мое знакомство с геометрией состоялось. Я узнал много нового: как родилась и развивалась эта наука, убедился, что многие профессии связаны с геометрическими знаниями, да и людям других профессий приходится сталкиваться с геометрией в обыденной жизни. Геометрия повсюду. Я понял, что геометрию обязательно нужно учить.

Подготовительные работы для ремонта в моей комнате закончены. Мне пришлось здорово потрудиться: я выполнял измерительные и расчетные работы, чтобы узнать, какие площади придется ремонтировать; много времени потратил, чтобы подобрать ремонтные материалы; производил расчеты количества и стоимости отделочных и ремонтных материалов. Конечно, без знания геометрии я бы не обошелся. Родители оценили мою работу, и ремонт в моей комнате вот-вот начнется.

Список использованной литературы

1. Геометрия в 7-9 классах, Л. С. Атанасян, Москва, «Просвещение», 2010

2. За страницами учебника математики, И.Я. Депман, Н.Я. Виленкин, «Дрофа», 2003

3. Математические кружки, И. С. Петраков, Москва, «Просвещение», 1987

4. Трудные разделы школьной математики, А. А. Черняк, Минск, «Красико-Принт»,

2003

5 . http://top.thepo.st/2150300/Poleznaya-geometriya

6. http://www.bibliofond.ru/view.aspx?id=555977#1

7. http://www.0zd.ru/matematika/istoriya_geometrii.html

Проект «Геометрия вокруг нас»

Министерство образования и науки Республики Дагестан

Республиканский конкурс исследовательских проектов младших

школьников «Первоцвет»

«Геометрия вокруг нас»

«Математика – царица наук»

Выполнила: МанаповаАмина , ученица 4 класса

ГКОУ РД «Бабаюртовская средняя школа-интернат №11»

Руководитель: Муслимова Зоя Алигаджиевна, учитель начальных классов.

Введение

Актуальность:На уроках математики мы изучали ромб треугольник, прямоугольник, окружность, квадрат — геометрические фигуры. А что же это за наука геометрия? Что же она изучает?Мы ученики четвертого класса стоим в начале пути в мир геометрии. На самом деле этот мир окружает нас с самого рождения. Так говорит нам наша учитель Зоя Алигаджиевна. Ведь, все что мы видим вокруг: дома, окна, загадочный узор снежинки, капля воды и даже камень на земле, так или иначе, все относится к геометрии, ничто не ускользает от её внимательного взгляда. Эпиграфом к своей работе я вяла высказывание великого французского архитектора Ле Корбюзье «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».
С геометрией мы встречаемся на каждом шагу, хотя и не обращаем на это внимание. Это наблюдение мне показалось очень интересным.

Исходя из выбранной темы я решила рассмотреть геометрические фигуры и тела в архитектурных объектах моего села.

Цель: научиться узнавать геометрические фигуры в обыденных предметах, изучить геометрию моего села.

Задачи:

Изучить историю возникновения геометрии.
Завести дневник проектной работы.
Проанализировать и сравнить предметы в жилище, в транспорте, в космосе, в природе на наличие геометрических фигур.
Исследовать геометрию села Бабаюрт.
Нарисовать рисунок с использованием геометрических предметов.

1. История возникновения геометрии.

Великий немецкий математик Вильгельм Лейбниц сказал:

«Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет».

Геометрия – что это? Спросила я у мамы. «Гео» означает «Земля», «метр» — это единица измерения длины. Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».
Заглянем в прошлое, когда зародилась наука геометрия….В «Энциклопедическом словаре юного математика» написано: «Геометрия – одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках».

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами. А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром.Но не только в процессе работы знакомились люди с геометрическими фигурами. Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).
Для того чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы.
Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д.Египетские пирамиды насчитывают 4800 лет, а их строительство, очевидно, требовало достаточно точных геометрических расчетов, так как состоят они из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра. Без математических знаний все эти сооружения невозможно было бы построить.

2. Разделы геометрии.

Геометрия состоит из двух частей: планиметрии и стереометрии.

Планиметрия – это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.

Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве.

Геометрические фигуры: точка, прямая, луч, отрезок, треугольник, квадрат, прямоугольник, окружность, трапеция, ромб…

Геометрические тела: прямоугольный параллелепипед, куб, шар, цилиндр, конус, пирамида…

3.Геометрия вокруг нас.

Все предметы в нашем доме напоминают различные геометрические фигуры. Это видно из дневника наблюдения, который я вела.

Заглянем на кухню. Холодильник, микроволновая печь, газовая плита, кухонный шкаф, стиральная машина имеют форму прямоугольного параллелепипеда. Потому, что как и у параллелепипеда все противолежащие грани прямоугольники их всего 6, 12 ребер, 8 вершин, есть три измерения – длина, ширина, высота. Лейка похожа на конус. Кастрюли цилиндрической формы. Тарелки напоминают круг, край тарелки — окружность. Крышка стола прямоугольник.Давайте заглянем вовнутрь холодильника и что же мы видим, и здесь без геометрии не обошлось. На полках стоят «цилиндры» — банка сгущенки, банка молока, консервы, кусок колбасы.

Знаете мама рассказала мне, что если поделить длину окружности на ее диаметр, то получится 3 с остатком. Я решила проверить это. Яблоко, апельсин, лук и тыква – вот, что я использовала.

Яблоко. Длина окружности – 25 см., диаметр – почти 8 см. 25:8=3(ост.1)

Апельсин. Длина окружности – 28 см., диаметр – почти 9 см. 28:9=3(ост.1)

Лук. Длина окружности – 16 см., диаметр – 5 см. 16:5=3(ост.1)

Тыква. Длина окружности – 95 см., диаметр – 31 см. 95:31=3(ост.2)

Вывод: Отношение длины окружности к её диаметру является одинаковымдля всех окружностей.

Прогуляемся по спальне. Шкаф, кровать, трельяж, стол – прямоугольные параллелепипеды. Ковер на полу прямоугольной формы. Горшки с цветами цилиндрической формы.

По улице движутся автомобили, трамваи, троллейбусы, велосипеды. Их колёса с геометрической точки зрения – круги. Сложную форму имеет корпус подводной лодки. Корпус космического спутника состоит из цилиндров. Сложную форму имеют и детали машин – гайки, винты, зубчатые колёса.

В самой природе очень много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой. Кристаллы горного хрусталя напоминают отточенный карандаш. Кристалл соли имеет форму куба. А снежинки – это одна из самых красивых геометрических фигур. Обычная горошина, капельки росы – имеют форму шара.

Животные, конечно, же геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел. Многие птицы строят гнёзда в форме полушара. Но самые искусные геометры – пчёлы. Они строят соты из шестиугольников.

Поиск геометрических фигур в предметах, которые нас окружают, был бы не полным, если бы мы не обратились к космическим объектам и не определили, форму каких фигур они имеют. Форма планет, звёзд – шарообразная. Планеты движутся вокруг солнца по траекториям, имеющим форму эллипса. Известно, что смена времён года на Земле происходит именно потому, что орбита Земли – эллипс. Таким образом в космическом пространстве находятся объекты только круглой или другой криволинейной формы и отсутствуют прямолинейные объекты.

4.Геометрия моего села.

А можно ли рассмотреть Бабаюрт как геометрический объект?

Если посмотреть на фотографию моего села, сделанную со спутника, которую я нашла в интернете, то территория занимаемая Бабаюртом напоминает мне треугольник.

Итак, я выхожу на улицу и вижу линии электропередач – разве они не похожи на параллельные прямые?!

Дорога по которой я иду каждый день в школу – это длинный прямоугольник.

Фасады домов – это одни прямоугольники и треугольники.

Мусорный бак – прямоугольный параллелепипед. Длина – 80 см. ширина – 80 см. Высота – 95 см.

В моем селе есть водозаборные башни. Теперь я знаю, что эти огромные бочки имеют цилиндрическую форму. Сколько же там воды? Спросила я у мамы. И вот что у нас получилось.

1 бочка. Длина – 5 метров, диаметр 3 метра. — это формула расчета объема цилиндра. Объем бочки получился около 35 тонн воды.

2 и 3 бочки (они одинаковые). Длина – 11 метров, диаметр – 2метра.Объем бочки получился около 35 тонн воды. Эти вычисления делала мама, но скоро и я научусь. Зато я могу посчитать количество воды в трех бочках. Таким образом запас воды 105 тонн.

Знаете в прошлом году у нас состоялось открытие парка, на территории которого имеется центр традиционной культуры народов России. Давайте заглянем туда.

Сама территория – это прямоугольник. Имеется 2 фонтана. Один имеет форму цилиндра, высотой 60 см. и диаметром 3 метра. Второй – восьмиугольник. Площадка для катания на роликах, снова прямоугольник, длина и ширина которого 25 и 7 метров.

В моем селе есть спорткомплекс «Атлант», само здание прямоугольный параллелепипед, окна, двери – прямоугольники. Посмотрите на фонари – это шар. Флагштоки напоминают параллельные прямые.А спортплощадка – это сплошные цилиндры.

По дороге мне встретились еще геометрические фигуры – это дорожные знаки. Окружность – парковка запрещена. Треугольник – уступи дорогу. Квадрат – пешеходный переход.

И вот я дошла до мечети. Она состоит из прямоугольного параллелепипеда и правильной 8-угольной призмы. Давайте заглянем во внутрь. Огромная комната длиной 30 м. и шириной 10 м. Площадь пола 300 м². если на 1 м²помещается 2 человека, то на пятничную молитву могут прийти 600 человек. На полу постелен очень красивый ковёр зеленого цвета, ширина его 1 метр. Если ширина комнаты 10 метров, то значит 10 рядов ковра. Мне стала интересна его длина. 10 раз по 30 метров – это 300 метров.

А какова же площадь мечети аль-Харам — главная и крупнейшая в мире мечеть, во внутреннем дворе которой находится главная святыня ислама — Кааба. И снова мне помог интернет.На данный момент общая площадь составляет 357 тыс. кв. метров и может вместить 2 500 000 человек.

5.Заключение.

В процессе проведения данной проектной работы яувидела, сколько самых разнообразных геометрических фигур, тел и поверхностей использует человек в своей повседневной жизни, в своей деятельности. Вокруг нас находится большое количество предметов, имеющих форму геометрических фигур. При исследовании по данной теме я добилась поставленных целей: не много узнала о истории геометрии, изучила геометрические фигуры вокруг нас. Подводя итог работы, пришла к выводу об актуальности данной темы. Невозможно представить современную жизнь без геометрических фигур, они вокруг нас, мы живем среди них, они нам нужны.

6.Литература:

Будько Т.С. Геометрические представления у дошкольников № 3, 1993.
История математики. Т. 1 /Ппод ред. Юшкевича А.Г. – М., 1970
Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
Энциклопедия для детей. Я познаю мир. Математика. – М: Издательство АСТ, 1999.
Ворошилов А.В. Математика и искусство. – М. просвещение, 1992. – 352
Рыбников К.А. История математики: Учебник. – М.: Изд-во МГУ, 1994. – 495 с
Энциклопедия для детей. Том 11. Математика. – М.: Аванта +, 1999.
http://nsportal.ru/detskii-sad/raznoe/skazka-o-geometricheskikh-figurakh
http://nsportal.ru/nachalnaya-shkola/blog/geometriya-v-nashei-zhizni
http://psiholog1.com/testy_dlya_vseh/test-risunok-chelovechka-iz-geometricheskix-figur.html
Энцеклопедический словарь юного натуралиста/ сост.А.Г Рогожкин. – М. : Педагогика,1981.
Энциклопедия для детей. Математика. – М. :Аванта +, 2003.Т, 11.
http: //ilib.mccme.ru/djvu/geometry/geom_ rapsodiya.htm/ — Левитин К.Ф. Геометрическая рапсодия.

Проектная работа «Геометрия вокруг нас «

Министерство образования и науки Республики Дагестан

Республиканский конкурс исследовательских проектов младших

школьников «Первоцвет»

«Геометрия вокруг нас»

«Математика – царица наук»

Выполнила: Манапова Амина , ученица 4 класса

ГКОУ РД «Бабаюртовская средняя школа-интернат №11»

Руководитель: Манапова Мадина Закарьяевна.

Введение

Актуальность: На уроках математики мы изучали ромб треугольник, прямоугольник, окружность, квадрат — геометрические фигуры. А что же это за наука геометрия? Что же она изучает? Мы ученики четвертого класса стоим в начале пути в мир геометрии. На самом деле этот мир окружает нас с самого рождения. Так говорит нам наша учитель Зоя Алигаджиевна. Ведь, все что мы видим вокруг: дома, окна, загадочный узор снежинки, капля воды и даже камень на земле, так или иначе, все относится к геометрии, ничто не ускользает от её внимательного взгляда. Эпиграфом к своей работе я вяла высказывание великого французского архитектора Ле Корбюзье «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».
С геометрией мы встречаемся на каждом шагу, хотя и не обращаем на это внимание. Это наблюдение мне показалось очень интересным.

Цель: научиться узнавать геометрические фигуры в обыденных предметах, изучить геометрию моего села.

Задачи:

Изучить историю возникновения геометрии.
Проанализировать и сравнить предметы в жилище, в транспорте, в космосе, в природе на наличие геометрических фигур.
Исследовать геометрию села Бабаюрт.
Нарисовать рисунок с использованием геометрических предметов.

1. История возникновения геометрии.

Великий немецкий математик Вильгельм Лейбниц сказал:

«Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет».

Геометрия – что это? Спросила я у мамы. «Гео» означает «Земля», «метр» — это единица измерения длины. Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».
Заглянем в прошлое, когда зародилась наука геометрия…. В «Энциклопедическом словаре юного математика» написано: «Геометрия – одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках».

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами. А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Но не только в процессе работы знакомились люди с геометрическими фигурами. Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).
Для того чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы.
Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д. Египетские пирамиды насчитывают 4800 лет, а их строительство, очевидно, требовало достаточно точных геометрических расчетов, так как состоят они из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра. Без математических знаний все эти сооружения невозможно было бы построить.

2. Разделы геометрии.

Геометрия состоит из двух частей: планиметрии и стереометрии.

Планиметрия – это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.

Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве.

Геометрические тела: прямоугольный параллелепипед, куб, шар, цилиндр, конус, пирамида…

3. Геометрия вокруг нас.

Заглянем на кухню. Холодильник, микроволновая печь, газовая плита, кухонный шкаф, стиральная машина имеют форму прямоугольного параллелепипеда. Потому, что как и у параллелепипеда все противолежащие грани прямоугольники их всего 6, 12 ребер, 8 вершин, есть три измерения – длина, ширина, высота. Лейка похожа на конус. Кастрюли цилиндрической формы. Тарелки напоминают круг, край тарелки — окружность. Крышка стола прямоугольник. Давайте заглянем вовнутрь холодильника и что же мы видим, и здесь без геометрии не обошлось. На полках стоят «цилиндры» — банка сгущенки, банка молока, консервы, кусок колбасы.

Яблоко. Длина окружности – 25 см., диаметр – почти 8 см. 25:8=3(ост.1)

Апельсин. Длина окружности – 28 см., диаметр – почти 9 см. 28:9=3(ост.1)

Лук. Длина окружности – 16 см., диаметр – 5 см. 16:5=3(ост.1)

Тыква. Длина окружности – 95 см., диаметр – 31 см. 95:31=3(ост.2)

Вывод: Отношение длины окружности к её диаметру является одинаковым для всех окружностей.

4.Геометрия моего села.

А можно ли рассмотреть Бабаюрт как геометрический объект?

Итак, я выхожу на улицу и вижу линии электропередач – разве они не похожи на параллельные прямые?!

Дорога по которой я иду каждый день в школу – это длинный прямоугольник.

Фасады домов – это одни прямоугольники и треугольники.

Мусорный бак – прямоугольный параллелепипед. Длина – 80 см. ширина – 80 см. Высота – 95 см.

1 бочка. Длина – 5 метров, диаметр 3 метра. V=π*R2 *h — это формула расчета объема цилиндра. Объем бочки получился около 35 тонн воды.

2 и 3 бочки (они одинаковые). Длина – 11 метров, диаметр – 2 метра. Объем бочки получился около 35 тонн воды. Эти вычисления делала мама, но скоро и я научусь. Зато я могу посчитать количество воды в трех бочках. Таким образом запас воды 105 тонн.

В моем селе есть спорткомплекс «Атлант», само здание прямоугольный параллелепипед, окна, двери – прямоугольники. Посмотрите на фонари – это шар. Флагштоки напоминают параллельные прямые. А спортплощадка – это сплошные цилиндры.

А какова же площадь мечети аль-Харам — главная и крупнейшая в мире мечеть, во внутреннем дворе которой находится главная святыня ислама — Кааба. И снова мне помог интернет. На данный момент общая площадь составляет 357 тыс. кв. метров и может вместить 2 500 000 человек.

5.Заключение.

В процессе проведения данной проектной работы я увидела, сколько самых разнообразных геометрических фигур, тел и поверхностей использует человек в своей повседневной жизни, в своей деятельности. Вокруг нас находится большое количество предметов, имеющих форму геометрических фигур. При исследовании по данной теме я добилась поставленных целей: не много узнала о истории геометрии, изучила геометрические фигуры вокруг нас. Подводя итог работы, пришла к выводу об актуальности данной темы. Невозможно представить современную жизнь без геометрических фигур, они вокруг нас, мы живем среди них, они нам нужны.

6.Литература:

Будько Т.С. Геометрические представления у дошкольников № 3, 1993.
История математики. Т. 1 /Ппод ред. Юшкевича А.Г. – М., 1970
Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
Энциклопедия для детей. Я познаю мир. Математика. – М: Издательство АСТ, 1999.
Ворошилов А.В. Математика и искусство. – М. просвещение, 1992. – 352
Рыбников К.А. История математики: Учебник. – М.: Изд-во МГУ, 1994. – 495 с
Энциклопедия для детей. Том 11. Математика. – М.: Аванта +, 1999.
http://nsportal.ru/detskii-sad/raznoe/skazka-o-geometricheskikh-figurakh
http://nsportal.ru/nachalnaya-shkola/blog/geometriya-v-nashei-zhizni
http://psiholog1.com/testy_dlya_vseh/test-risunok-chelovechka-iz-geometricheskix-figur.html
Энцеклопедический словарь юного натуралиста/ сост.А.Г Рогожкин. – М. : Педагогика,1981.
Энциклопедия для детей. Математика. – М. : Аванта +, 2003.Т, 11.
http: //ilib.mccme.ru/djvu/geometry/geom_ rapsodiya.htm/ — Левитин К.Ф. Геометрическая рапсодия.

Исследовательская работа по математике «Геометрия моего города»

Слайд 1

ГЕОМЕТРИЯ МОЕГО ГОРОДА Выполнила студентка Ивановского железнодорожного колледжа Ермакова А. Преподаватель Мочалова Е.В.

Слайд 2

Знаменитому архитектурному реформатору Ле Корбюзье принадлежит авторство восторженного высказывания, настоящего гимна геометрии: «Окружающий нас мир – это мир геометрии чистой, истинной, безупречной в наших глазах. Все вокруг – геометрия. Никогда мы не видим так ясно таких форм, как круг, прямоугольник, угол, цилиндр, выполненных с такой тщательностью и так уверенно». Обоснование темы

Слайд 3

Проблемный вопрос: Где «живет» геометрия в нашем городе? Цели и задачи проекта: углубить знания по геометрии, в частности, по стереометрии, так как в архитектуре как раньше, так и сейчас используются различные геометрические фигуры и тела; рассмотреть наш город с геометрической точки зрения; показать на примерах разнообразие архитектурных объектов нашего города; создать слайд — шоу «Геометрические объекты в архитектуре нашего города»

Слайд 4

Геометрические формы в архитектуре нашего города Для работы над проектом я рассмотрела следующие геометрические понятия, фигуры и их совокупность: взаимное расположение прямых в пространстве, многогранники и тела вращения, симметрия, асимметрия, многоугольники и плоские кривые – и попыталась увидеть их в архитектурных сооружениях города Иваново.

Слайд 5

С высоты птичьего полета территория города похожа на эллипс При более детальном рассмотрении четко видны параллельные, перпендикулярные и пересекающиеся прямые улиц города

Слайд 6

На фото со спутника кажется, что на Минеевском мосту проспект Ленина пересекается с железной дорогой, а в действительности – это скрещивающиеся прямые.

Слайд 7

Географический центр города – «нулевой километр». Столбик, обозначающий нулевой километр в Иваново, установлен у почтамта. В основе знака – усеченная четырехугольная пирамида.

Слайд 8

Главной архитектурной достопримечательностью города считается один из его символов – Щудровская палатка , самая старая гражданская кирпичная постройка Иваново. Здание представляет собой прямоугольный параллелепипед

Слайд 9

Успенская церковь — православная деревянная церковь клетского типа. Составлена из четырех прямоугольных срубов-клетей, покрытых двускатными кровлями. Шатровое (в виде пирамиды) покрытие часовни, купол в форме луковки (тело вращения).

Слайд 10

Это общественное здание, построенное в стиле конструктивизма. Состоит из нескольких призм, поставленных друг на друга. Здание театрального комплекса

Слайд 11

Ивановский цирк. Основное здание – восьмиугольная прямая призма объединенная с четырехугольной призмой. Здание имеет внутренний двор в форме треугольного колодца. На крыше здания расположен шаровой сегмент с надписью «Цирк».

Слайд 12

Дом-корабль. Здание построено в 1930 году и интересно, прежде всего, своей необычной архитектурой, внешним видом напоминающей корабль. С одной стороны прямоугольное пятиэтажное здание имеет скошенный торец, к противопо-ложной стороне пристроена восьмиэтажная башня (призма).

Слайд 13

Дом-подкова является одним из многочисленных памятников советского конструктивизма в городе и объектом культурного наследия регионального значения. Если смотреть на дом сверху, его форма напоминает подкову (дугу) .

Слайд 14

Усадьба Дюрингера — уголок средневековой Европы в небольшом уездном городке центральной России. Наиболее интересный модернистский проектом архитектора Снурилова. Главными особенностями стиля модерн стали стремление к мягким, природным линиям в противовес классическим прямым, использование новых материалов (стекла, металла), переосмысление архитектурных стилей и их взаимное сочетание в одном объекте. В этом комплексе мы видим и цилиндрическую башню , и асимметричную крышу , и различной формы окна.

Слайд 15

Здание медицинской академии. На Шереметьевском проспекте находится здание ИГМА, построенное в стиле классицизм с элементами ампира. Три четырехугольные призмы , цилиндрические колонны, арочная форма окон второго яруса, шпили в форме конусов и пирамид , аудиторный корпус в форме прямоугольного параллелепипеда можно увидеть в этом архитектурном объекте.

Слайд 16

Здание стоматологической поликлиники №1 построено в стиле неоклассицизма с элементами московского модерна. Основная часть здания имеет три этажа и форму неправильного прямоугольника. Угол фасада , выходящий на пересечение улиц, округлен и понижен до двух этажей. Здесь расположен центральный вход в здание, который оформлен тремя арками . Просторный круглый холл на первом этаже стал композиционным ядром внутреннего интерьера. Примечательным делает это здание, также небольшая башня над главным входом с куполообразной крышей .

Слайд 17

Симметрия – важная составляющая архитектурных стилей Зеркальная симметрия Зеркальная симметрия Осевая симметрия Зеркальная симметрия Центральная симметрия Осевая симметрия

Слайд 18

Кривые в архитектурных объектах окружность Спираль Архимеда Логарифмическая кривая кардиода Часто

Слайд 19

Заключение Все архитектурные сооружения города Иваново состоят из геометрических фигур и их совокупностей. Чаще встречается – параллелепипед, такую форму имеют все жилые дома и различные учреждения. Это объясняется в первую очередь тем, что такая форма более удобна для проживания, проще при строительстве . Но развитие строительной индустрии позволяет создавать здания более сложных, интересных форм, придающих индивидуальность каждому объекту. Геометрия украшает город, придает ему строгость, индивидуальность и красоту.

Что такое геометрия? Когда вы используете это в реальном мире?

Геометрия — одна из классических дисциплин математики. Примерно перевод в переводе с греческого как «Измерение Земли», это связано со свойствами пространство и цифры. В первую очередь он разработан как практическое руководство для измерения длин, площадей и объемов, которые используются до сих пор. Евклид превратил изучение геометрии в аксиоматическую форму примерно в 3 веке До н.э., и эти аксиомы актуальны и по сей день.Важно Эволюция науки о геометрии была создана, когда Рене Декарт был смог создать концепцию аналитической геометрии. Из-за этого самолет цифры теперь можно представить аналитически, и это одна из движущих сил для развития математического анализа. Кроме того, рост перспектив дал восхождение к проективной геометрии. В настоящее время современная геометрия тесно связана с физика, и является неотъемлемой частью новых физических концепций, таких как теория относительности и теории струн.

Самая основная форма геометрии — так называемая евклидова геометрия.Здесь рассматриваются длины, площади и объемы. Окружности, радиусы и площади являются одним из понятий, касающихся длины и площади. Также объем Трехмерные объекты, такие как кубы, цилиндры, пирамиды и сферы, могут вычисляться с использованием геометрии. Раньше все касалось форм и размеров, но числа скоро перейдут в геометрию. Благодаря пифагорейцам, числа вводятся в геометрию в виде числовых значений длин и районы. Числа используются далее, когда Декарт смог сформулировать понятие координат.

В реальной жизни геометрия имеет множество практических применений, начиная с самых простых. к самым передовым явлениям в жизни. Даже самая базовая концепция площади может быть огромным фактором в вашем повседневном бизнесе. Например, пробел это огромная проблема при планировании различных строительных проектов. Например, размер или площадь конкретного прибора или инструмента могут сильно повлиять на то, как он впишется в ваш дом или на рабочее место и может повлиять на то, как другие части вашего дома поместится вокруг него.Вот почему так важно учитывать областей, как вашего пространства, так и предмета, который вы собираетесь интегрировать там. Кроме того, геометрия играет важную роль в основных инженерных проектах. Например, используя концепцию периметра, вы можете вычислить сумму материала (например, краски, материала для ограждений и т. д.), который необходимо использовать для ваш проект. А также дизайнерские профессии, такие как дизайн интерьера и архитектура. использует 3-х мерные фигуры. Доскональное знание геометрии поможет помочь им в определении правильного стиля (и, что более важно, оптимизировать его функция) конкретного дома, здания или транспортного средства.

Это некоторые из наиболее простых применений геометрии, но на этом все не заканчивается. Поскольку еще некоторые профессии используют геометрию для правильного выполнения своей работы. Например, компьютерное изображение, то, что сегодня используется для создания анимации, видеоигры, дизайн и тому подобное создаются с использованием геометрические понятия. Также геометрия используется при картографировании. Картирование — это очень важно элемент в таких профессиях, как геодезия, навигация и астрономия. Из от эскизов до расчета расстояний, они используют геометрию для выполнения своих работа.Кроме того, геометрические изображения приносят пользу в таких профессиях, как медицина. Такие технологии, как компьютерная томография и МРТ, используются как для диагностики, так и для хирургии. СПИД. Такие методы позволяют врачам выполнять свою работу лучше, безопаснее и проще.

Как видите, геометрия влияет на нас даже в самых элементарных деталях нашего жизни. Независимо от формы, он помогает нам понять конкретные явления. и это помогает нам повышать качество жизни.

Сайты для изучения геометрии

Энциклопедия центров треугольника
Евклида Доказательство теоремы Пифагора-
Основы геометрии
Геометрия Сфера
Галерея интерактивного Онлайн-геометрия
Геометрический Теория групп
Геометрия Формулы и факты
Геометрия в действии
Свалка Геометрии
Математические кривые и поверхности

Simple English Wikipedia, бесплатная энциклопедия

Геометрия — это раздел математики, изучающий размер, форму, положение и размеры предметов. Мы можем видеть или создавать только плоские (2D) или твердые (3D) формы, но математики (люди, изучающие математику) могут изучать формы, которые являются 4D, 5D, 6D и так далее.

Квадраты, круги и треугольники — одни из самых простых форм в плоской геометрии. Кубы, цилиндры, конусы и сферы — это простые формы в твердой геометрии.

Геометрия плоскости может использоваться для измерения площади и периметра плоской формы. С помощью твердотельной геометрии можно также измерить объем и площадь твердой формы.

С помощью геометрии можно вычислить размер и форму многих предметов. Например, геометрия может помочь людям найти:

Геометрия — один из старейших разделов математики. Геометрия зародилась как искусство исследования земли, чтобы люди могли справедливо разделить ее. Слово «геометрия» происходит от греческого слова, которое означает «измерить землю».Из этого он превратился в одну из важнейших частей математики. Греческий математик Евклид написал первую книгу о геометрии, книгу под названием The Elements .

Плоская и твердотельная геометрия, описанная Евклидом в его учебнике «Элементы», называется «Евклидовой геометрией». На протяжении веков это называлось просто «геометрией». В 19 веке математики создали несколько новых видов геометрии, которые изменили правила евклидовой геометрии. Эти и более ранние виды назывались «неевклидовыми» (не созданы Евклидом).Например, гиперболическая геометрия и эллиптическая геометрия возникли в результате изменения постулата Евклида о параллельности.

Неевклидова геометрия сложнее евклидовой геометрии, но имеет множество применений. Например, сферическая геометрия используется в астрономии и картографии.

Геометрия начинается с нескольких простых идей, которые считаются верными и называются аксиомами. Такие как:

Точка отображается на бумаге путем прикосновения к ней карандашом или ручкой без каких-либо боковых движений.Мы знаем, где находится точка, но у нее нет размера.
Прямая линия — это кратчайшее расстояние между двумя точками. Например, Софи тянет веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.
Плоскость — это плоская поверхность, которая не останавливается ни в каком направлении. Например, представьте себе стену, которая бесконечно простирается во всех направлениях.

Викискладе есть медиафайлы, связанные с Geometry .

Рубрики

Геометрия в нашем доме: Проект по математике «Геометрические фигуры в моем доме»

Проект по математике «Геометрические фигуры в моем доме»

Муниципальное бюджетное общеобразовательное учреждение Покровская средняя школа

Ухоловского муниципального района Рязанской области 391923,Рязанская область, Ухоловский район, с. Покровское, ул. Школьная, д. 19, тел. 5 -54-10

Проект по геометрии «Геометрия вокруг нас»

Проект по геометрии «Занимательная геометрия».

Научно-практическая работа «Геометрия в нашей жизни»

Проект «Геометрия вокруг нас»

Проектная работа «Геометрия вокруг нас «

Исследовательская работа по математике «Геометрия моего города»

Что такое геометрия? Когда вы используете это в реальном мире?

Что такое геометрия? Когда вы используете это в реальном мире?

Сайты для изучения геометрии

Simple English Wikipedia, бесплатная энциклопедия

Добавить комментарий Отменить ответ