Что такое правильный треугольник: Что такое правильный треугольник? Ответ на webmath.ru
Радиусы $r$ и $R$, вписанной и описанной окружностей равностороннего треугольника, связаны с длиной его стороны $a$ следующими соотношениями:
$$r=\frac{\sqrt{3}}{6} a, \quad R=\frac{\sqrt{3}}{3} a$$Примеры решения задач
Пример
Задание. Найти, чему равна высота равностороннего треугольника со стороною $a = 4$ см.
Решение. Сделаем рисунок (рис. 2).
Высота в равностороннем треугольнике является так же и медианой, поэтому:
$A H=H C=\frac{1}{2} A C=2$
Далее, рассмотрим $\Delta B H C$, этот треугольник прямоугольный. По теореме Пифагора:
$$B H=\sqrt{B C^{2}-H C^{2}}$$
то есть
$B H=\sqrt{4^{2}-2^{2}}=\sqrt{16-4}=\sqrt{12}=2 \sqrt{3}$ (см)
Ответ.
{2}=\frac{27 \cdot 4}{3}=36 \\
a=\sqrt{36}=6 \\
a=6
\end{array}
$$
Ответ. $a = 6$ дм.
Пример
Задание. Дан равносторонний треугольник $ABC$, со стороной $a=6 \sqrt{3}$ см. Найти радиусы вписанной и описанной окружностей.
Решение. Сделаем рисунок (рис. 3).
Радиус $r$ вписанной и радиус $R$ описанной окружностей равностороннего треугольника связаны с его длиной $a$ следующими соотношениями:
$$r=\frac{\sqrt{3}}{6} a, \quad R=\frac{\sqrt{3}}{3} a$$
Подставляя значение $a=6 \sqrt{3}$, получим:
$r=\frac{\sqrt{3} \cdot 6 \sqrt{3}}{6}=3(\mathrm{~cm}) \quad, \quad R=\frac{\sqrt{3} \cdot 6 \sqrt{3}}{3}=6$ (см)
Ответ. $r = 3$ см , $R = 6$ см
Читать дальше: что такое средняя линия треугольника.
Правильный треугольник – формулы
Средняя оценка: 4.6
Всего получено оценок: 103.
Обновлено 11 Января, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
Обновлено 11 Января, 2021
Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.
Рис. 1. Правильный треугольник.Формулы правильного треугольника
Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.Площадь
Начнем с формулы площади.
Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.
Рис. 2. Рисунок к доказательству.В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
$$Sin(ВАM)={ВM\over AB}$$
С другой стороны синус 60 градусов заранее известнее и равен $\sqrt{3} \over 2$ . Значит можно выразить значение АМ:
$$ВМ=АВ*sin(ВАM)=AB* {\sqrt{3}\over 2}$$
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
AB=AC=BC=a
Тогда формула будет выглядеть следующим образом:
$$ВМ=а*{\sqrt{3}\over2}$$
Теперь вспомним классическую формулу площади треугольника:
$S= {1\over2}h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию.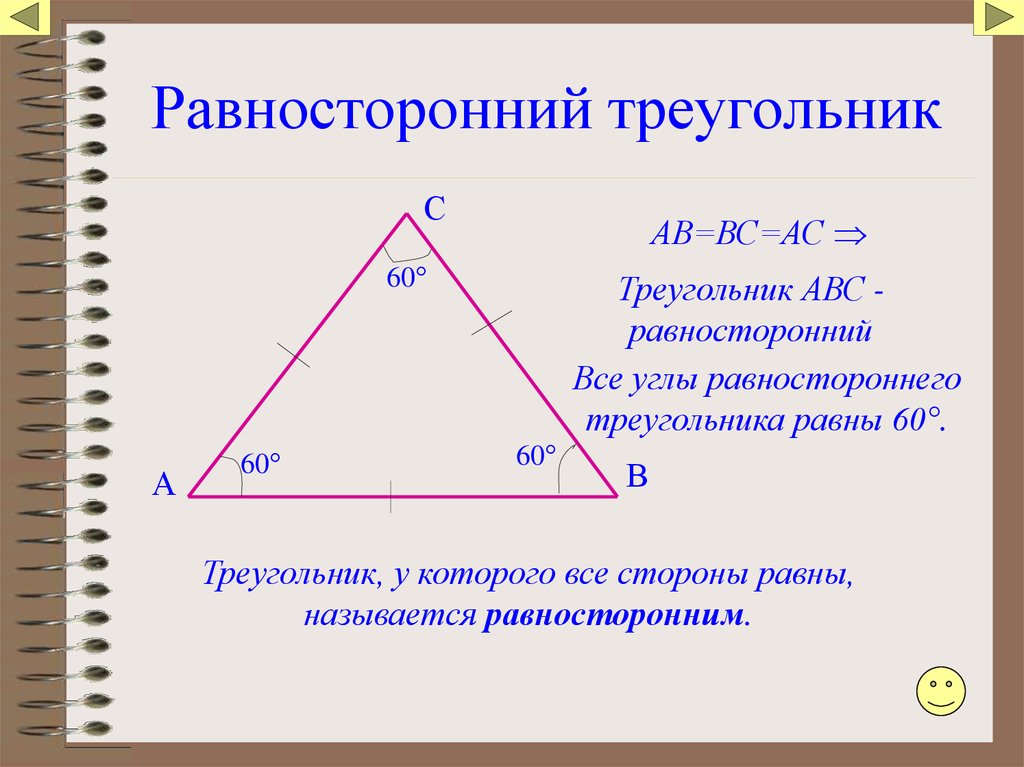
2*{\sqrt{3}\over4}$$
Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади через значение одной стороны.
Периметр
Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:Р=3а
Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.
В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.
Что мы узнали?
Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Иван Дарьин
5/5
Василий Головин
5/5
Денис Каспер
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
А какая ваша оценка?
Прямоугольный треугольник — формула, определение, свойства, факты
Треугольник, в котором один из внутренних углов равен 90°, называется прямоугольным треугольником. Самая длинная сторона прямоугольного треугольника, которая также является стороной, противоположной прямому углу, — это гипотенуза, а две стороны прямого угла — это высота и основание.
Вот как выглядит прямоугольный треугольник:
Общая площадь или территория, покрываемая прямоугольным треугольником, известна как площадь прямоугольного треугольника. Он рассчитывается в квадратных единицах. Единицы м 2 , cm 2 , in 2 , yd 2 и другие обычно представляют площадь.
Особенности прямоугольного треугольника
- Прямой угол всегда является наибольшим углом в прямоугольном треугольнике.
- Гипотенуза, сторона, противоположная прямому углу, является самой длинной стороной.
- В прямоугольном треугольнике не может быть тупых углов.
Типы прямоугольных треугольников
В широком смысле прямоугольные треугольники можно разделить на следующие категории:
1. Равнобедренный прямоугольный треугольник : В этом треугольнике один внутренний угол равен 90°, а два других угла равны 45° каждый. Он также известен как треугольник 45-90-45.
Это равнобедренный прямоугольный треугольник, стороны которого AB и AC равны, а ∠ B составляет 90°.
Здесь ∠ A и ∠ C имеют по 45° каждый, потому что свойство гласит, что углы, противоположные равным сторонам, также равны.
2. Разносторонний прямоугольный треугольник : В этом треугольнике один внутренний угол равен 90°, а два других имеют разную величину. Например:
В прямоугольном треугольнике ABC ∠ A составляет 30°, ∠ B составляет 90°, а ∠ C составляет 60°. В этом треугольнике все три стороны будут разной длины и три угла будут разной величины.
Формула прямоугольного треугольника
Теорема Пифагора
- Пифагор обнаружил, что квадрат гипотенузы равен сумме квадратов двух других сторон прямоугольного треугольника.
Периметр прямоугольного треугольника
Периметр прямоугольного треугольника определяется как общая длина границы. Формула для периметра:
P (периметр) = a + b + c (сумма сторон треугольника)
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника определяется как пространство, занимаемое треугольником.
Формула площади:
Площадь = $\frac{1}{2}\times base\time height$
Решенные примеры
- Самая большая сторона треугольника равна 10 см. Если высота треугольника 8 см, определите площадь по теореме Пифагора.
Решение:
Гипотенуза — самая длинная сторона прямоугольного треугольника.
Здесь гипотенуза ( H ) = 10 см, высота ( h ) = 8 см и основание ( b ) неизвестно.
Согласно теореме Pythagoras,
H 2 = B 2 + H 2
2 = B 2 + 2 = B 2 + 9 9 2 69 = 3 B 2 + 2 . 100 = b 2 + 64
b 2 = 36 см 2
b = = $\sqrt{6}0003
Площадь = $\frac{1}{2}\times base\times height$
= $\frac{1}{2}\times 6\times 8 = 24$
Следовательно, площадь треугольника = 24 квадратных см.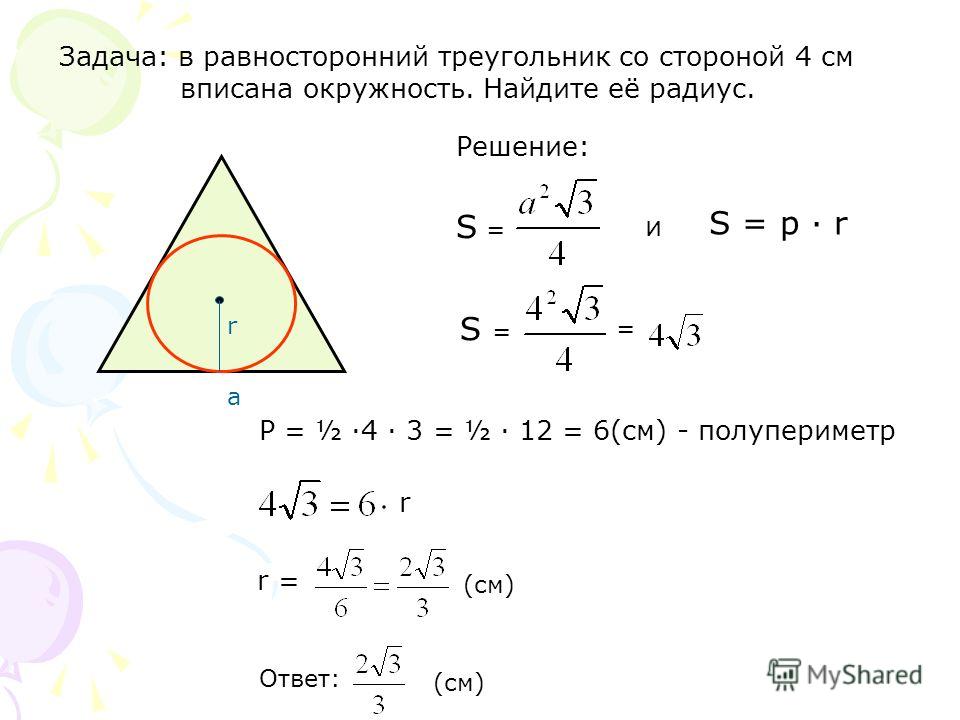
- Соотношение сторон треугольника 3:4:5. Периметр 840 м. Найдите его площадь.
Решение :
Пусть стороны треугольника равны 3 x , 4 x и 5 x соответственно.
Мы знаем, что периметр = 840 м.
3 x + 4 x + 5 x = 840
12 x = 840
x = $ \ frac {840} {12} $ = 70
SO, SI -SIVE треугольника:
3 х = 3(70) = 210 м
4 х = 4(70) = 280 м
5 х = 5(70) 9003 м 350 м — самая длинная сторона треугольника, это гипотенуза.
Итак, 210 м и 280 м — это основание и высота треугольника взаимозаменяемо.
Используя формулу площади прямоугольного треугольника, получаем
Площадь = $\frac{1}{2}\times base\times height = \frac{1}{2}\times 210\times 280 = 29,400$
Следовательно, площадь данного треугольника = 29,400 м 2
- Какова мера гипотенузы в прямоугольном треугольнике, высота которого равна 7 см, а основание равно 5 см?
Решение:
Перпендикулярная высота ( h ) = 7 см, основание ( b ) = 5 см и Гипотенуза ( H ) = ?
By Pythagoras Theorem,
H 2 = b 2 + p 2
H 2 = 5 2 + 7 2
H 2 = 25 + 49
H 2 = 74
H = $ \ SQRT {74} $ CM
Практические задачи
1
в правой Angle Triang и b = 32, а периметр треугольника равен 58 см.
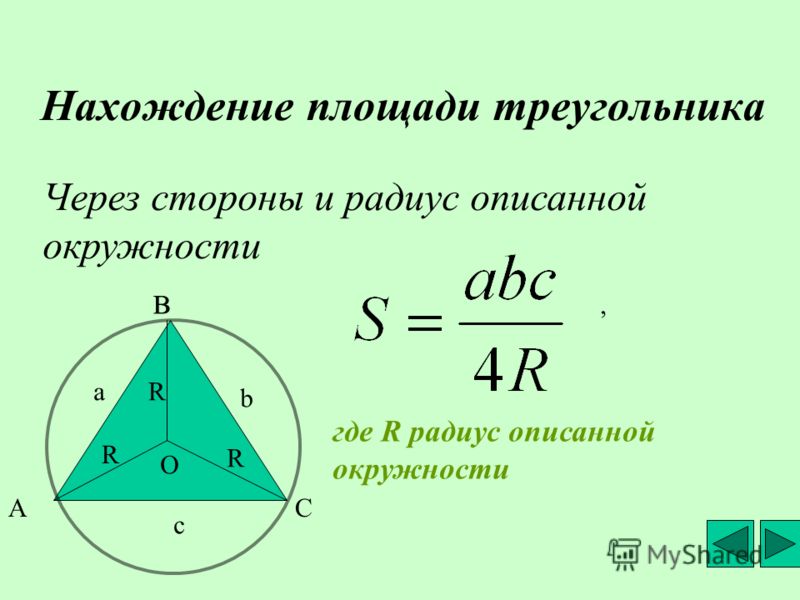Найдите с, третью сторону треугольника.44 см
50 см
12 см
14 см
Правильный ответ: 14 см
58 = 12 + 32 + c, c = 14 см = 23 см, ВС = 14 см, СА = 13 см. Чему равен периметр треугольника?
234 см
33 см
50 см
40 см
Правильный ответ: 50 см
Периметр = (23 + 14 + 13) см = 50 см Высота прямоугольного треугольника с гипотенузой 13 см и основанием 5 см? 92} = \sqrt{16 + 9} = \sqrt{25}$ = 5 см
Часто задаваемые вопросы
Может ли прямоугольный треугольник иметь две равные стороны?
Прямоугольный треугольник также может быть равнобедренным, что означает, что у него две стороны и два угла равны. Прямоугольный равнобедренный треугольник имеет угол 90° и два угла по 45°.
Могут ли 8 см, 15 см и 17 см составлять три стороны прямоугольного треугольника?
Мы можем проверить, образуют ли 8 см, 15 см и 17 см три стороны прямоугольного треугольника, используя теорему Пифагора.
H (Hypotenuse) 2 = P (Perpendicular height) 2 + B (Base) 2
172 = 152+82
289 = 225 + 64
289 = 289
Отсюда проверено, что 8 см, 15 см и 17 см могут составить три стороны прямоугольного треугольника.
Как называются 3 стороны прямоугольного треугольника?
Основание, перпендикулярная высота и гипотенуза — три стороны прямоугольного треугольника.
Какая формула Пифагора для прямоугольного треугольника?
Теорема Pythagoras гласит следующую формулу для правого треугольника: H (гипотенуза) 2 = P (перпендикулярная высота) 2 + B (База) 2
rhip rough — Формула, определение, свойства
Прямоугольный треугольник — это треугольник, один из углов которого равен 90 градусов. Угол в 90 градусов называется прямым углом, поэтому треугольник с прямым углом называется прямоугольным.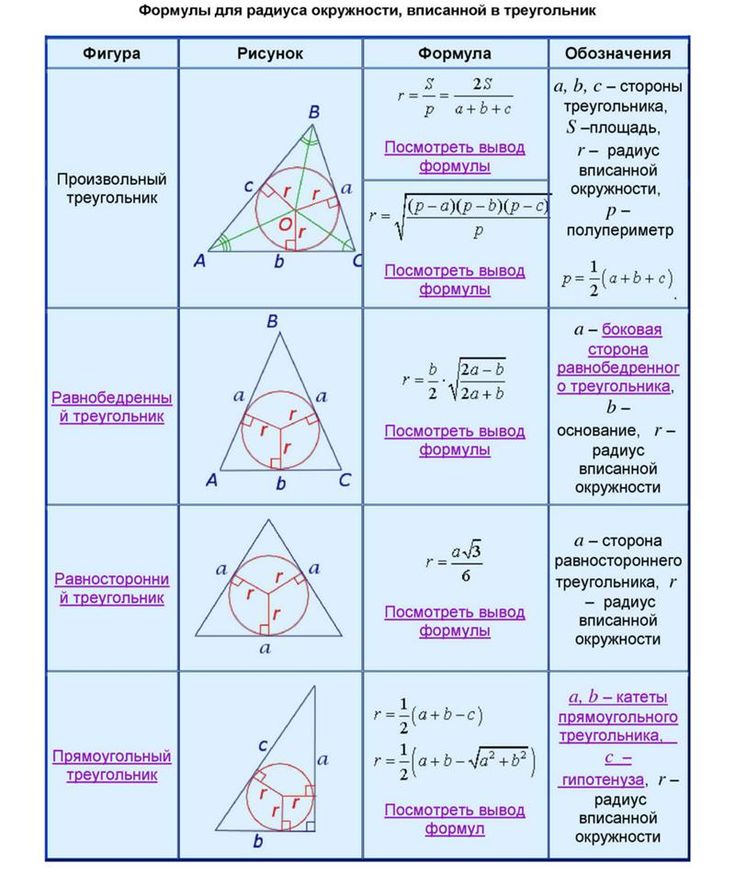
В этом треугольнике отношения между различными сторонами можно легко понять с помощью правила Пифагора. Сторона, противоположная прямому углу, является наибольшей стороной и называется гипотенузой. Кроме того, на основании других значений углов прямоугольные треугольники классифицируются как равнобедренный прямоугольный треугольник и разносторонний прямоугольный треугольник. Также длины сторон прямоугольного треугольника, такие как 3, 4, 5, называются тройками Пифагора.
| 1. | Что такое прямоугольный треугольник? |
| 2. | Формула прямоугольного треугольника |
| 3. | Периметр прямоугольного треугольника |
| 4. | Площадь прямоугольного треугольника |
| 5. | Свойства прямоугольного треугольника |
| 6. | Типы прямоугольных треугольников |
| 7. | Часто задаваемые вопросы о прямоугольном треугольнике |
Что такое прямоугольный треугольник?
Определение прямоугольного треугольника гласит, что если один из углов треугольника является прямым углом — 90º, такой треугольник называется прямоугольным треугольником или просто прямоугольным треугольником.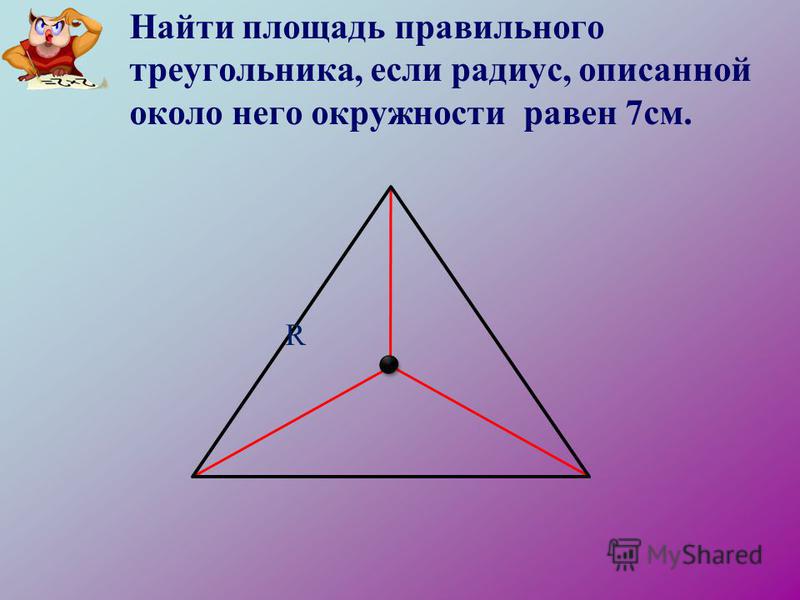
Здесь мы можем понять отличительные черты прямоугольного треугольника. Характеристики треугольника ABC следующие:
- AC высота, высота или перпендикуляр
- AB является базовым
- АС ⊥ АВ
- ∠А=90º
- Сторона ВС, противоположная прямому углу, называется гипотенузой и является наибольшей стороной прямоугольного треугольника.
Примерами прямоугольных треугольников в нашей повседневной жизни являются треугольный ломтик хлеба, квадратный лист бумаги по диагонали или 30-60-90 треугольная шкала в окне геометрии.
Формула прямоугольного треугольника
Великий греческий философ Пифагор вывел важную формулу для прямоугольного треугольника.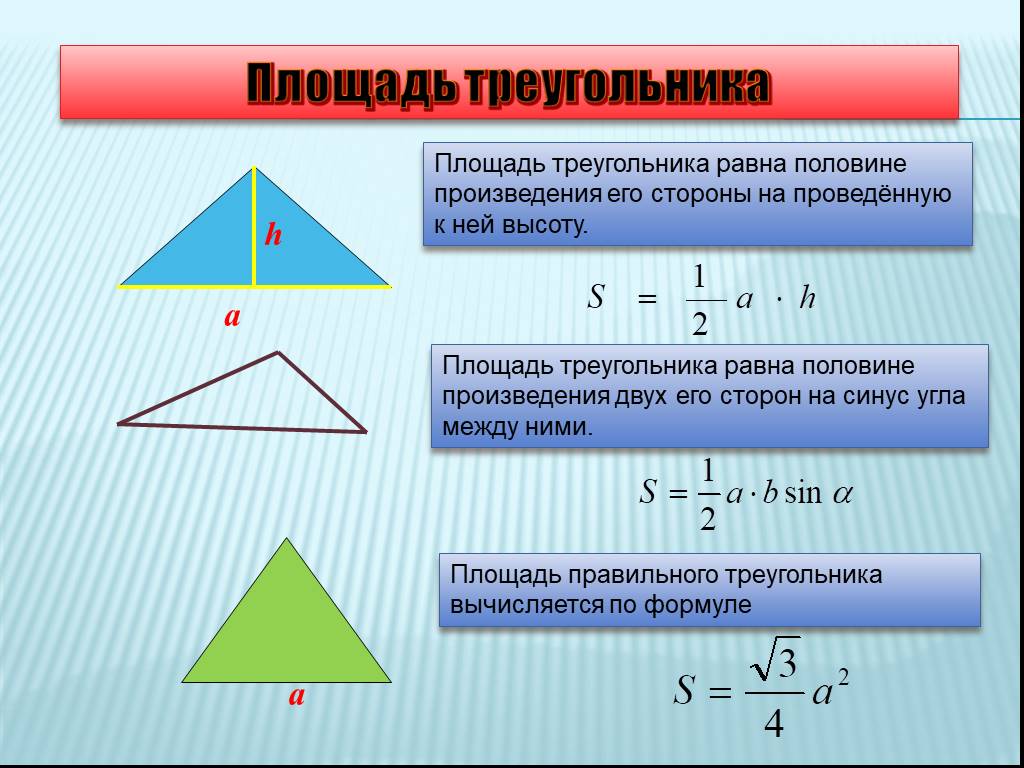
Формула гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других катетов. Она была названа в его честь теоремой Пифагора. Формулу прямоугольного треугольника можно представить следующим образом: Квадрат гипотенузы равен сумме квадрата основания и квадрата высоты .
В прямоугольном треугольнике мы имеем: (Гипотенуза) 2 = (Основание) 2 + (Высота) 2
Триплет Пифагора : Три числа, которые удовлетворяют приведенному выше уравнению, являются триплетами Пифагора. Например, (3, 4, 5) является пифагорейской тройкой, потому что мы знаем, что 3 2 = 9, 4 2 = 16 и 5
Периметр прямоугольного треугольника
Периметр прямоугольного треугольника равен сумме мер всех трех сторон.
Это сумма основания, высоты и гипотенузы прямоугольного треугольника. Здесь для нижнего прямоугольного треугольника периметр равен сумме сторон BC + AC + AB = (a + b + c) единиц. Периметр является линейной величиной и имеет единицу длины.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника определяет ширину или пространство, занимаемое треугольником. Он равен половине произведения основания и высоты треугольника. Это двумерная величина и поэтому представлена в квадратных единицах. Единственные две стороны, необходимые для нахождения площади прямоугольного треугольника, — это основание и высота.
Применяя определение прямоугольного треугольника, площадь прямоугольного треугольника определяется по формуле: Площадь прямоугольного треугольника = (1/2 × основание × высота) квадратных единиц.
Свойства прямоугольного треугольника
Первое свойство прямоугольного треугольника состоит в том, что один из его углов равен 90º.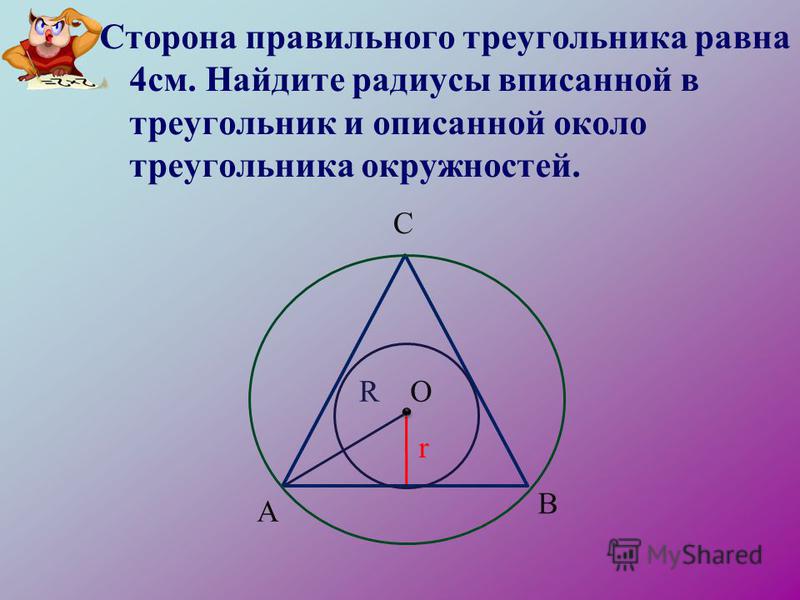
Угол 90º является прямым углом и наибольшим углом прямоугольного треугольника. Кроме того, два других угла меньше 90º или являются острыми углами. Свойства прямоугольного треугольника перечислены ниже:
- Наибольший угол всегда равен 90º.
- Самая большая сторона называется гипотенузой, которая всегда является стороной, противоположной прямому углу.
- Стороны измеряются по правилу Пифагора.
- У него не может быть тупого угла.
Типы прямоугольных треугольников
Мы узнали, что один из углов прямоугольного треугольника равен 90º. Это означает, что два других угла в треугольнике будут острыми углами. Есть несколько особых прямоугольных треугольников, а именно равнобедренных прямоугольных треугольников и разносторонних прямоугольных треугольников . Треугольник, у которого два других угла равны, называется равнобедренным прямоугольным треугольником, а треугольник, у которого два других угла имеют разные значения, называется разносторонним прямоугольным треугольником.
Равнобедренный прямоугольный треугольник
Равнобедренным прямоугольным треугольником называется треугольник с углами 90°-45°-45°. В треугольнике ABC угол A = 90º; поэтому по определению прямоугольного треугольника треугольник ABC является прямоугольным. Также АВ = АС; так как две стороны равны, треугольник также является равнобедренным треугольником. Так как АВ = АС, то углы при основании равны. Мы знаем, что сумма углов треугольника равна 180º. Следовательно, сумма углов при основании равна 9.0º, что означает, что они по 45º каждая. Так в равнобедренном прямоугольном треугольнике углы всегда будут 90º-45º-45º.
Разносторонний прямоугольный треугольник
Разносторонний прямоугольный треугольник — это треугольник, в котором один угол равен 90°, а два других угла до 90° имеют разные измерения. В треугольнике PQR ∠Q =90º, следовательно, это прямоугольный треугольник. PQ не равен QR, следовательно, это разносторонний треугольник. Существует также особый случай разностороннего треугольника 30º-60º-90º, который также является прямоугольным треугольником, в котором отношение самой длинной стороны треугольника к его самой короткой стороне составляет 2: 1.
Сторона, противоположная углу 30º, является самой короткой стороной.
Советы и рекомендации
Здесь перечислены некоторые важные советы и рекомендации, касающиеся прямоугольного треугольника.
- Измерения длин сторон всегда удовлетворяют теореме Пифагора.
- В прямоугольном треугольнике гипотенуза — это сторона, противоположная прямому углу, и это самая длинная сторона треугольника.
- Две другие ноги перпендикулярны друг другу; один — основание, а другой — высота.
Важные примечания
- В прямоугольном треугольнике (гипотенуза) 2 = (основание) 2 + (высота) 2
- Площадь прямоугольного треугольника равна 1/2 × основание × высота.
- Периметр прямоугольного треугольника равен сумме мер всех трех сторон.
- Равнобедренных прямоугольных треугольников имеют градусные меры 90º, 45º, 45º.
Похожие темы
Проверьте эти статьи, связанные с понятием прямоугольного треугольника.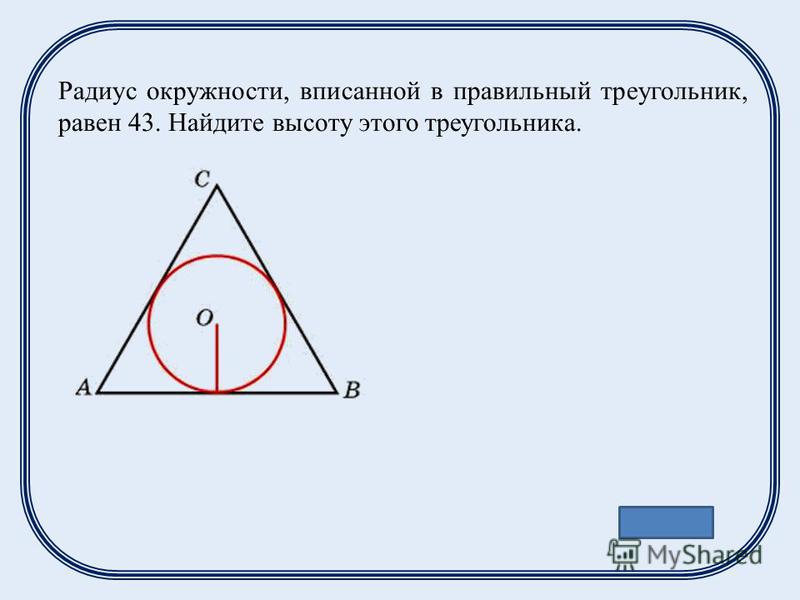
- Гипотенуза
- Пифагорейская тройка
- Формула гипотенузы
Примеры прямоугольного треугольника
Пример 1: Может ли прямоугольный треугольник иметь размеры 11 дюймов, 60 дюймов и 61 дюйм?
Решение:
Если числа 11, 60 и 61 являются пифагоровой тройкой, они образуют прямоугольный треугольник. 11 2 = 121; 60 2 = 3600; 61 2 = 3721. Мы видим, что: 121 + 3600 = 3721. Следовательно, данные числа являются пифагоровой тройкой и могут быть размерами прямоугольного треугольника. Следовательно, 11 дюймов, 60 дюймов и 61 дюйм образуют прямоугольный треугольник.
Пример 2: Найдите площадь прямоугольного треугольника, основание которого равно 12 единицам, а высота 5 единицам.
Решение:
Формула площади треугольника равна 1/2 × b × h. Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 .
Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.Пример 3: Периметр прямоугольного бассейна составляет 720 единиц. Три стороны бассейна находятся в соотношении 3:4:5. Найдите площадь бассейна.
Решение:
Периметр прямоугольного треугольника равен сумме мер всех его сторон. Следовательно, 3x+4x+5x = 720
. 12х = 720
х = 60
Стороны треугольника 3x=180 единиц, 4x=240 единиц и 5x=300 единиц. С 1809 г.0005 2 + 240 2 = 300 2 , эти стороны образуют прямоугольный треугольник с гипотенузой 300 единиц. Следовательно, площадь бассейна составляет 1/2 × 180 × 240 = 21600 единиц 2 . Таким образом, площадь бассейна составляет 21600 квадратных единиц.
Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по прямоугольным треугольникам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о прямоугольном треугольнике
Что такое прямоугольный треугольник в геометрии?
Треугольник, в котором одна из мер углов равна 90 градусов, называется прямоугольным треугольником или прямоугольным треугольником.
Какие существуют типы прямоугольных треугольников?
Треугольники классифицируются на основе измерения сторон и углов. Ниже перечислены три типа прямоугольных треугольников.
- Равнобедренный прямоугольный треугольник — это треугольник, в котором углы равны 90º, 45º и 45º.
- Разносторонний прямоугольный треугольник — это треугольник, в котором один угол равен 90°, а два других острых угла имеют разную величину.
- Треугольник 30º — 60º — 90º — еще один интересный прямоугольный треугольник, в котором отношение самой длинной стороны треугольника к его самой короткой стороне составляет 2:1.
Какова мера углов прямоугольного треугольника?
У прямоугольного треугольника один из углов равен 90º. Два других угла острые. И все три угла прямоугольного треугольника в сумме дают 180°, как и любого другого треугольника.
Какая формула прямоугольного треугольника?
Для прямоугольного треугольника используется формула Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон. Формула Пифагора: (Гипотенуза) 2 = (Основание) 2 < + (Высота) 2 . Эта формула дала триплеты Пифагора, такие как 3, 4, 5.
Как найти площадь прямоугольного треугольника?
Площадь прямоугольного треугольника – это площадь, занимаемая треугольником, и равна половине произведения основания и высоты треугольника. Он двумерный и представлен в квадратных единицах.
Площадь прямоугольного треугольника = 1/2 × основание × высота в квадрате
Может ли прямоугольный треугольник иметь две равные стороны?
Да, прямоугольный треугольник может иметь две равные стороны.