Треугольник в интерьере: Треугольники в дизайне и декоре

• О проекте

• Заказать дизайн-проект
• Каталог мебели и аксессуаров
  • 
  • 
  • 
    
• Гид по стилю
• Советы
  • • Все Советы
    • Дизайн интерьера
    • Декор
    • Ремонт и планировка
    • Хэнд-мэйд
  • Дизайн интерьера 17.08.2020

    Детская комната в чёрном цвете – взгляд изнутри

  • Дизайн интерьера 13.08.2020

    Светильники в современном стиле: актуальный светодизайн

  • Дизайн интерьера
    23.07.2019

    Светильники в скандинавском стиле: путешествие в страну фьордов

  • Дизайн интерьера 13.07.2019

    Светильники в японском стиле: постигаем дзен

  • Ремонт и планировка
    09.07.2019

    Виды отделки потолка: характеристики и дизайн

  • Дизайн интерьера 17.08.2020

    Детская комната в чёрном цвете – взгляд изнутри

  • Дизайн интерьера
    13.08.2020

    Светильники в современном стиле: актуальный светодизайн

  • Дизайн интерьера 23.07.2019

    Светильники в скандинавском стиле: путешествие в страну фьордов

  • Дизайн интерьера 13.07.2019

    Светильники в японском стиле: постигаем дзен

  • Дизайн интерьера
    05.07.2019

    Светильники в английском стиле: во власти традиций

  • Декор 02.04.2019

    Настенный декор в скандинавском стиле: особенности и идеи

  • Декор

своими руками, просто и быстро

Настоящая Мебель

2015-09-05T00:00:00+03:0013:1105.09.2015 13:11:41

Для того чтобы воплотить эту идею, понадобятся только краска двух-трех оттенков и малярная лента.

1. Возьмите малярную ленту и наклейте ее прямыми линиями в самых разных направлениях – как вашей душе угодно, с любым количеством пересечений, больших и маленьких треугольников.

2. Покрасьте всю стену полностью одним основным цветом и дайте ей высохнуть.

3. Возьмите краску другого оттенка и закрасьте несколько отдельных треугольников в произвольном порядке. Можно выбрать оттенок в одной цветовой гамме с основным цветом, а можно добавить контраста и сделать несколько ярких треугольников, повторяющих цветовые акценты интерьера комнаты.

4. Когда краска высохнет, снимите малярную ленту со стены.

5. Стена готова.

Такая четкая геометрия в интерьере выглядит довольно стильно. Оцените ее противоположность – градиентную покраску стен с естественными, мягкими переходами.

Треугольник в фэн шуй: значение и применение символа

В древнекитайском учении фэншуй есть не только позитивные, но и негативные символы, которых нужно стремится избегать или хотя бы пытаться минимизировать их негативное значение. Один из таких символов – треугольник. Он изобилует острыми углами, чего китайцы в принципе не любят – считается, что на таких углах создаются завихрения энергии, которая трансформируется из положительной в отрицательную, то есть, из Ци в Ша.

Но если треугольник по фэншую расположить правильно, то толк будет и от него. А если в правильных местах использовать красный треугольник, то никакого вреда точно не будет. Но обо всем по порядку.

Треугольник – символ по феншуй

Согласно этому учению, разным природным стихиям соответствуют разные геометрические формы, а именно:

• Огню – треугольник,
• Земле – квадрат,
• Воде – волнистая линия,
• Металлу – круг,
• Дереву – прямоугольник.

Это важно знать, оформляя помещения – расставляя мебель, планируя ниши и различные детали интерьера.

Согласно сетке ба гуа, огонь – символ южного сектора, отвечающего за славу и репутацию. Цвет этого сектора – красный.

Вот почему использовать треугольные формы и углы можно только в южной (а также в юго-западной) части квартиры. Если же треугольные фигуры или мебель с такими углами разместить на западе или в северо-западном секторе, то дом покинут удача и процветание.

Очень хорошо, если у дома крыша имеет форму правильного треугольника – тогда его жильцов ждет удача и успех во всем. Но никаких других треугольных фигур с острыми углами рядом с домом использовать не стоит – ни новомодных фигурных скамеек, ни клумб, ни даже придверных ковриков. Положительный эффект может иметь только объемная пирамидальная фигура, где треугольник служит всего лишь одной из сторон. Красную пирамиду располагают на приусадебном участке в южном его секторе, если хотят добиться видного положения в обществе.

Красный треугольник феншуй

Чтобы активировать зону славы и репутации, используются красные треугольники феншуй. Это один из самых удачных вариантов для данного сектора.

Материал изготовления – любой, кроме бумаги и дерева, так как им не место в зоне огня.

Располагается треугольник одним из углов вверх. В таком положении он поможет:

• Добиться успеха во всех начинаниях,
• Завоевать положительную репутацию,
• Реализовать амбициозные планы,
• Добраться до самой вершины в своем деле.

Нет ограничений по поводу того, использовать ли равнобедренный или какой-то другой треугольник. Важно только правильно его разместить. Можно повесить его на стену, а можно использовать в качестве настольной фигуры при помощи специальной подставки.

Чтобы сделать интерьер комнаты менее скучным, парень решил украсить стену треугольными полками: получилось очень стильно

Этот парень решил что-нибудь изменить в интерьере своей комнаты, чтобы пространство выглядело не таким скучным. У него появилась отличная идея и он своими руками сделал полки в виде треугольников. Это оказалось очень легко, а результат получился стильным и современным.

Материалы и инструменты

Для создания полки в виде геометрической фигуры молодому человеку понадобились следующие материалы:

• Клей для дерева.
• Лист фанеры.
• Краска и кисти.

Кроме того, ему пришлось приобрести шлифовальный станок, дрель, устройство для забивания гвоздей, а также настольную пилу. Все эти предметы продаются в строительных магазинах практически во всех населенных пунктах. Стоит отметить, что все зависит от вашего воображения, поэтому вам может понадобиться краска различных оттенков.

Кстати, вы можете приобрести кронштейны, если хотите, чтобы полки могли выдерживать относительно тяжелые вещи.

Подготовка фанеры

Для начала необходимо подготовить фанеру. Молодой человек использовал материал толщиной около 2 см. При помощи пилы он разрезал лист на несколько полос шириной около 10 см. Затем он разрезал каждую из получившихся полос на три доски с углами 30 градусов на концах. Их длина составила 45 см. На самом деле их размеры могут быть любыми, все зависит от ваших предпочтений.

Следующим шагом была обработка фанеры. Сначала парень отшлифовал ее при помощи электрического инструмента. Затем решил покрасить одну из внутренних сторон серой краской, чтобы она немного выделялась. Как раз оставалось немного пигмента после ремонта, он-то и пошел в дело.

Собираем полки

Наконец, пришло время собирать полки. Сначала могут возникнуть проблемы с соединением углов, но если обработать края клеем, то они должны сразу исчезнуть.

Кроме того, после применения клея парень устанавливал на все стыки финишные гвозди, которые надежно их скрепляли.

Осталось дело за малым — повесить получившиеся треугольники на стены. Для этого парень вбил в стены гвозди. Поскольку такие полки не предназначены для тяжелых предметов, достаточно одного металлического элемента для их поддержки. Впрочем, при желании всегда можно установить кронштейны под дно.

Разместить полки можно несколькими способами: основанием вниз, вверх или их комбинацией. В данном случае одна из них была установлена вершиной вниз, а по бокам от нее висели полки-треугольники в более привычном виде.

Вот такое украшение для стены получилось у парня. Комната сразу приобрела более стильный вид и перестала быть скучной.

А вы бы хотели что-то подобное?

Нашли нарушение? Пожаловаться на содержание

Геометрические узоры в интерьере: 6 фигур для дизайна

Все фигуры делятся на два типа: прямолинейные и криволинейные. К первому типу относится квадрат, прямоугольник, треугольник и т.п. К криволинейным: круг, овал.

Квадраты и прямоугольники

Эти две фигуры еще со школы ассоциируются у нас с четкостью и правильностью. Использование в интерьере прямоугольников и квадратов создает ощущение надежности и стабильности. 

Прямые линии зрительно увеличивают, расширяют пространство. Если хотите, чтобы ваш потолок визуально стал ниже, то деление его на квадраты – то, что нужно. Например, декоративные балки, прикрепленные к потолку, в прямом смысле слова опустят его. 

Не зря говорят, что горизонтальная полоска «полнит». Горизонтальные полосы зрительно расширяют комнату и «занижают» потолок при этом. Такой вариант идеален для маленьких помещений. С полосой они выглядят просторнее.

Помните, чем шире полоса, тем меньше заметен визуальный эффект. Если комнату надо вытянуть в высоту или ширину, используйте не очень широкую полосу. Только не переусердствуйте, слишком узкая может рябить.

Детская – одно из любимых мест для использования полосы. Здесь она как никогда уместна – жизнерадостный узор, всегда в моде, к тому же не придется переклеивать, как слоников или жирафов.

Овалы и круги

Овалы и круги – крупный брат “горошка”. Очень спокойный и гармоничный узор и хорошо со всем сочетается. Подобно полоскам, круги и овалы идеально впишутся в детскую комнату. Визуальное спокойствие узора делает его хорошим выбором и для спальни.

Зигзаги

Как правило, зигзаг предстает ярким, динамичным и ни на кого не похожим. Психологи утверждают, что такие узоры помогают обретать вдохновение и чувствовать прилив сил, даже если человек очень устал. Зигзаг удачно сочетается с другими геометрическими фигурами и может вписаться практически в любой интерьер.

Зигзаг может быть на обоях, шторах, коврах, подушках, мебели, столах, где угодно. 

Ромбы

Ромб или «Аргайл» (второе название такого типа узора), берет свое начало в Шотландии. Нетрудно догадаться, что основывался он на шотландской клетке. Поначалу такой узор начал набирать популярность в Англии, а затем уже в США, где использовался в качестве принтов на одежде. 

Вскоре ромбы перешли и на другие предметы. Чаще всего ромбы встречаются в качестве рисунка на текстиле: постельном белье, подушках, шторах, пледах и т.д. Иногда из него делают акцент на обоях, как в примере на фото ниже. Это хорошее решение для современной классики и минимализма.

Треугольники

Бытует мнение, что острые углы вызывают чувство тревоги и опасности. Мы не совсем с этим согласны. Использование треугольного орнамента рядом с предметами, имеющими закругленные углы, прекрасно дополнит интерьер и уравновесит его.

Да, слишком активное использование треугольного орнамента не приветствуется. Но в качестве акцента – на крупных предметах мебели, шторах, на предметах мебели или на одной акцентной стене – треугольник незаменим.

Какой из этого можно сделать вывод? Геометрия важна не только в школе, но и в интерьере, геометрические узоры универсальны, ненавязчивы, эффектны. Поэтому использовать их стоит, но с осторожностью. 

Единственный пункт, который может вам помешать украсить интерьер квадратами и ромбами – масштаб. Рисунок может оказаться слишком крупным, или, наоборот, рябить своей мелкотой. Поэтому будьте внимательны и пользуйтесь нашей статьей об орнаментах на этот случай.

Геометрия в дизайне интерьера | Личный блог дизайнера

Геометрические фигуры не первый сезон в моде, вот и 2018 год они не обошли стороной. Асимметрия и геометрические формы живут в отделке фасадов мебели, на настенных покрытиях и даже на паркете.

Мода на геометрию в интерьере, была характерно для 60-х годов.

Сегодня же, их используют в большей степени  в современном стиле или в скандинавском. Стиль «геометрия» в интерьере можно увидеть  в различных видах:

• Геометрия на плоскостях.
• Геометрия в мебели
• Геометрия в аксессуарах

Геометрия на плоскостях.

 Простое добавление геометрических фигур и диагональных линий действительно может показать особенность стены, и вы можете поэкспериментировать с цветом для дополнительного эффекта. «Оставайтесь в одной цветной схеме, чтобы вы не подавляли комнату, — говорит  эксперт по дизайну Dulux Андреа Лусена-Орра. «Здесь вы видите, что оттенки этих цветов — все это от группы красного цвета. Они хорошо работают вместе и дополняют геометрический рисунок, не создавая калейдоскоп цветов, что влияет на ощущение пространства».

 В черно-белых сочетаниях, основное эмоциональное воздействие создает именно форма. Поэтому контурные рисунки и штрихи могут придать абсолютно разный характер помещению. Геометрические узоры на стенах сегодня появляются, как в виде нарисованных узоров. Популярный выбор также – обои «геометрия» в интерьере, которые могут быть размещены только на одной стене, например, за спинкой кровати.

 Геометрические узоры в интерьере – и классические, и современные – также можно найти на полу. Они доминируют в основном в ванных комнатах и ​​кухнях в виде двухцветной, в основном черно-белой мозаики.

Геометрия в мебели.

 Огромное количество известных брендов и малознакомых производств используют геометрию для создания современной мебели. Треугольники, ромбы и многоугольниками — на основе этих фигур возникают необычные кресла, причудливые столики и необычные стулья. Такая мебель выглядит очень динамично, она всегда притягивает взгляд. Поэтому, надо быть осторожным, чтобы не перегрузить пространство! И, кстати, в этом вам сможет помочь компетентный взгляд дизайнера.

Геометрия в аксессуарах.

 Прекрасным решением станет приобретение подушек, пледов или покрывал, а также картин, панно и керамики с такими принтами. Замечательным дополнением к минималистскому стилю однотонной расцветки, станут кухонные полотенца, шторы, ковры. Также это актуально для скандинавских стилей.

 В заключение, хочется сказать, что геометрические мотивы распространяются не только на жилые интерьеры, но и общественные помещения.

 Скорее всего, ближайшие сезоны эта тенденция не изменится, переходя от одной цветовой комбинации к другой ещё длительное время.

Facebook

Twitter

Вконтакте

Google+

треугольников в геометрии (определение, типы, свойства и примеры)

• • Классы
    • Класс 1-3
    • Класс 4-5
    • Класс 6-10
    • Класс 11-12
  • КОНКУРСНЫЙ ЭКЗАМЕН
    • BNAT 000 NC
      • 000 NC Книги
        • Книги NCERT для класса 5
        • Книги NCERT для класса 6
        • Книги NCERT для класса 7
        • Книги NCERT для класса 8
        • Книги NCERT для класса 9
        • Книги NCERT для класса 10
        • Книги NCERT для класса 11
        • Книги NCERT для класса 12
      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT 9000 9000
        • NCERT Exemplar Class
          • Решения RS Aggarwal, класс 12
          • Решения RS Aggarwal, класс 11
          • Решения RS Aggarwal, класс 10
          90 003 Решения RS Aggarwal класса 9
          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • RD Sharma Class 6 Решения
          • Решения RD Sharma
          Решения RD Sharma Class 8
          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12
        • PHYSICS
          • Механика
          • Оптика
          • Термодинамика Электромагнетизм
        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица
        • MATHS
          • Теорема Пифагора
          0004
          • 000300030004
          • Простые числа
          • Взаимосвязи и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Деление фракций
        • 000
        • 000
        • 000
        • 000
        • 000
        • 000 Microology
        • 000
        • 000 Microology
        • 000 BIOG3000
          FORMULAS
          • Математические формулы
          • Алгебраические формулы
          • Тригонометрические формулы
          • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы
            • 0003000 PBS4000
            • 000300030002 Примеры калькуляторов химии
            Класс 6
            • Образцы бумаги CBSE для класса 7
            • Образцы бумаги CBSE для класса 8
            • Образцы бумаги CBSE для класса 9
            • Образцы бумаги CBSE для класса 10
            • Образцы бумаги CBSE для класса 11
            • Образцы бумаги CBSE чел для класса 12
          • CBSE Контрольный документ за предыдущий год
            • CBSE Контрольный документ за предыдущий год Класс 10
            • Контрольный документ за предыдущий год CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Class 11 Physics
            • Решения HC Verma, класс 12, физика
          • Решения Лакмира Сингха
            • Решения Лакмира Сингха, класс 9
            • Решения Лакмира Сингха, класс 10
            • Решения Лакмира Сингха, класс 8
          • Заметки CBSE
          • , класс
            CBSE Notes
            Примечания CBSE класса 7
            • Примечания CBSE класса 8
            • Примечания CBSE класса 9
            • Примечания CBSE класса 10
            • Примечания CBSE класса 11
            • Примечания CBSE класса 12
            • Примечания к редакции CBSE
              • Примечания к редакции
              • CBSE
              • Примечания к редакции класса 10 CBSE
              • Примечания к редакции класса 11 CBSE 9000 4
              • Примечания к редакции класса 12 CBSE
            • Дополнительные вопросы CBSE
              • Дополнительные вопросы по математике класса 8 CBSE
              • Дополнительные вопросы по науке 8 класса CBSE
              • Дополнительные вопросы по математике класса 9 CBSE
              • Дополнительные вопросы по науке класса 9 CBSE
              Дополнительные вопросы по математике для класса 10
              • Дополнительные вопросы по науке, класс 10 по CBSE
            • CBSE, класс
              • , класс 3
              • , класс 4
              • , класс 5
              • , класс 6
              • , класс 7
              • , класс 8
              • , класс 9 Класс 10
              • Класс 11
              • Класс 12
            • Учебные решения
          • Решения NCERT
            • Решения NCERT для класса 11
              • Решения NCERT для класса 11 по физике
              • Решения NCERT для класса 11 Химия
              Решения для биологии класса 11
              • Решения NCERT для математики класса 11
              9 0003 NCERT Solutions Class 11 Accountancy
              • NCERT Solutions Class 11 Business Studies
              • NCERT Solutions Class 11 Economics
              • NCERT Solutions Class 11 Statistics
              • NCERT Solutions Class 11 Commerce
            • NCERT Solutions For Class 12
              • NCERT Solutions For Класс 12 по физике
              • Решения NCERT для химии класса 12
              • Решения NCERT для класса 12 по биологии
              • Решения NCERT для класса 12 по математике
              • Решения NCERT Класс 12 Бухгалтерия
              • Решения NCERT, класс 12, бизнес-исследования
              • Решения NCERT, класс 12 Экономика
              • NCERT Solutions Class 12 Accountancy Part 1
              • NCERT Solutions Class 12 Accountancy Part 2
              • NCERT Solutions Class 12 Micro-Economics
              • NCERT Solutions Class 12 Commerce
              • NCERT Solutions Class 12 Macro-Economics
            • NCERT Solutions For Класс 4
              • Решения NCERT для математики класса 4
              • Решения NCERT для класса 4 EVS
            • Решения NCERT для класса 5
              • Решения NCERT для математики класса 5
              • Решения NCERT для класса 5 EVS
            • Решения NCERT для класса 6
              • Решения NCERT для математики класса 6
              • Решения NCERT для науки класса 6
              • Решения NCERT для социальных наук класса 6
              • Решения NCERT для класса 6 Английский
            • Решения NCERT для класса 7
              • Решения NCERT для класса 7 Математика
              • Решения NCERT для класса 7 Наука
              • Решения NCERT для класса 7 по социальным наукам
              • Решения NCERT для класса 7 Английский
            • Решения NCERT для класса 8
              • Решения NCERT для класса 8 Математика
              • Решения NCERT для класса 8 Science
              • Решения NCERT для социальных наук 8 класса
              • Решение NCERT ns для класса 8 Английский
            • Решения NCERT для класса 9
              • Решения NCERT для социальных наук класса 9
            • Решения NCERT для математики класса 9
              • Решения NCERT для математики класса 9 Глава 1
              • Решения NCERT для Математика класса 9 Глава 2
              • Решения NCERT для математики класса 9 Глава 3
              • Решения NCERT для математики класса 9 Глава 4
              Решения NCERT
              • для математики класса 9 Глава 5
              • Решения NCERT для математики класса 9 Глава 6
              • Решения NCERT для Математика класса 9 Глава 7
              • Решения NCERT для математики класса 9 Глава 8
              • Решения NCERT для математики класса 9 Глава 9
              Решения NCERT
              • для математики класса 9 Глава 10
              • Решения NCERT для математики класса 9 Глава 11
              • Решения NCERT для Математика класса 9 Глава 12
              • Решения NCERT для математики класса 9 Глава 13
              Решения
              • NCERT для математики класса 9 Глава 14
              • Решения NCERT для математики класса 9 Глава 15
            • Решения NCERT для науки класса 9
              • Решения NCERT для науки класса 9 Глава 1
              • Решения NCERT для науки класса 9 Глава 2
              • Решения NCERT для класса 9 Наука Глава 3
              • Решения NCERT для Науки Класса 9 Глава 4
              • Решения NCERT для Науки Класса 9 Глава 5
              • Решения NCERT для Науки Класса 9 Глава 6
              • Решения NCERT для Науки Класса 9 Глава 7
              • Решения NCERT для Класса 9 Наука, глава 8
              • Решения NCERT для науки 9 класса
              • Решения NCERT для науки класса 9 Глава 10
              • Решения NCERT для науки класса 9 Глава 12
              • Решения NCERT для науки класса 9 Глава 11
              • Решения NCERT для класса 9 Наука Глава 13
              • Решения NCERT для класса 9 Наука Глава 14
              • Решения NCERT для класса 9 по науке Глава 15
            • Решения NCERT для класса 10
              • Решения NCERT для класса 10 по социальным наукам
            • Решения NCERT для математики 10 класса
              • Решения NCERT для математики класса 10 Глава 1
              • Решения NCERT для математики класса 10 Глава 2
              • Решения NCERT для математики класса 10 Глава 3
              • Решения NCERT для математики класса 10 Глава 4
              • Решения NCERT для математики класса 10 Глава 5
              • Решения NCERT для математики класса 10 Глава 6
              • Решения NCERT для математики класса 10 Глава 7
              Решения NCERT
              • для математики класса 10 Глава 8
              • Решения NCERT для математики класса 10 Глава 9
              Решения NCERT
              • для математики класса 10 Глава 10
              Решения NCERT
              • для математики класса 10 Глава 11
              • Решения NCERT для математики класса 10 Глава 12
              • Решения NCERT для математики класса 10 Глава 13
              • NCERT Sol Решения NCERT для математики класса 10 Глава 14
              • Решения NCERT для математики класса 10 Глава 15
            • Решения NCERT для науки класса 10
              • Решения NCERT для науки класса 10 Глава 1
      .

      Incenter of A Triangle. Определено с примерами и изображениями

      Определение

      центра треугольника

      Центр центра — это одна из точек параллелизма треугольника, образованная пересечением трех биссектрис треугольника.

      Эти три биссектрисы угла всегда совпадают, а всегда пересекаются внутри треугольника (в отличие от ортоцентра, который может или не может пересекаться внутри треугольника). Инцентр — это центр вписанной окружности.Центр центра — это одна точка в треугольнике, расстояния до сторон которой равны. (См. Рисунок)

      • Если треугольник тупой, как, например, тот, что на картинке ниже слева, то центр центра расположен внутри треугольника.
      • Если треугольник острый, центр центра также находится внутри треугольника.
      Центр острого треугольника Центр тупого треугольника

      А как насчет центра прямоугольного треугольника?

      Покажи ответ

      Ответ

      На иллюстрациях выше показано, что центр тупого и острого треугольников расположен внутри.Итак, вопрос в том, где в прямоугольном треугольнике находится инцентр?

      Центр инкорпорации всегда расположен внутри треугольника, независимо от типа треугольника.

      Окружность треугольника

      Вписанная окружность треугольника — это самый большой круг, который вписывается в треугольник, а его центр — это центр. Его центр — это одна точка внутри треугольника, которая находится на равном расстоянии от всех сторон треугольника (см. Первое изображение ниже).

      Схема, показывающая вписанную окружность на одинаковом расстоянии с каждой стороны

      Фотографии вписанного круга

      .

      Калькулятор треугольников

      Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.

      Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

      

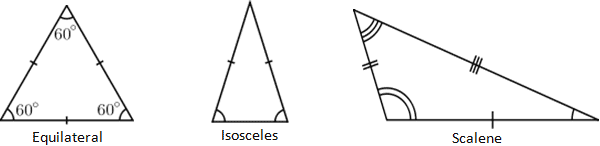
      Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину.Аналогичные обозначения существуют для внутренних углов треугольника, которые обозначаются разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из треугольников выше, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда введены фактические значения, выходные данные калькулятора будут отражать то, как должна выглядеть форма входного треугольника.

      Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.

      

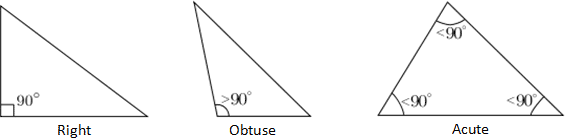
      Факты, теоремы и законы о треугольнике

      

      • Учитывая длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.

      

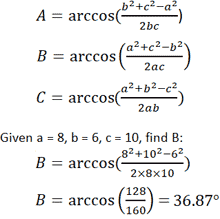
      Площадь треугольника

      Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h . «Основание» относится к любой стороне треугольника, где высота представлена ​​длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.

      

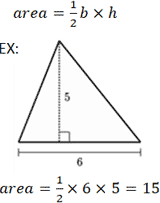
      Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:

      

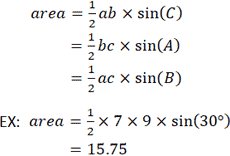
      Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:

      

      Медиана, внутренний радиус и радиус окружности

      Медиана

      Медиана треугольника определяется как длина отрезка прямой, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.См. Рисунок ниже для пояснения.

      

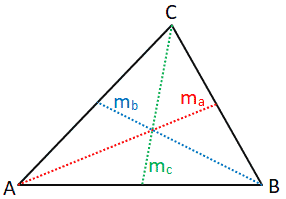
      Медианы треугольника представлены отрезками m _a , m _b и m _c . Длину каждой медианы можно рассчитать следующим образом:

      

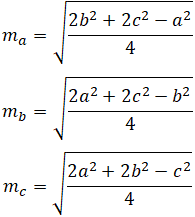
      Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.

      В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m _a может быть рассчитана следующим образом:

      

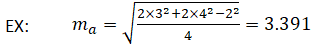
      Inradius

      Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это перпендикулярное расстояние между центром вращения и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.

      

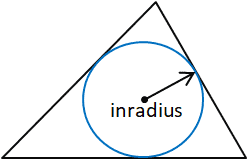
      В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:

      , где a, b и c — стороны треугольника

      Круговой радиус

      Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.

      

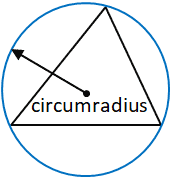
      В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:

      Где a — сторона треугольника, а A — угол, противоположный стороне a

      Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.

      .

      Равнобедренный треугольник — определение математического слова

      Равнобедренный треугольник — определение математического слова — Math Open Reference Треугольник, две стороны которого равны. Попробуйте это Перетащите оранжевые точки на каждую вершину, чтобы изменить форму треугольника. Обратите внимание, что он всегда остается равнобедренным треугольником, стороны AB и AC всегда равны по длине. Слово равнобедренное произносится как «глаз- sos -ell-easy» с ударением на «sos». Это любой треугольник с двумя сторонами одинаковой длины.

      Если все три стороны имеют одинаковую длину, это называется равносторонний треугольник. Очевидно, что все равносторонние треугольники также обладают всеми свойствами равнобедренного треугольника.

      Недвижимость

      • Неравную сторону равнобедренного треугольника обычно называют «основанием» треугольника.
      • Углы основания равнобедренного треугольника всегда равны. На рисунке выше углы ∠ABC и ∠ACB всегда одинаковы.
      • Когда 3-й угол является прямым, он называется «прямоугольный равнобедренный треугольник».
      • Высота — это расстояние по перпендикуляру от основания до самой верхней вершины.

      Построение равнобедренного треугольника

      Можно построить равнобедренный треугольник заданных размеров, используя только циркуль и линейку. Посмотрите на эти три конструкции:

      Решение равнобедренного треугольника

      Основание, катет или высота равнобедренного треугольника можно найти, если вы знаете два других. А серединный перпендикуляр базы образует высота треугольника, как показано справа.Это образует два совпадающие прямоугольные треугольники это можно решить с помощью Теорема Пифагора как показано ниже.

      Нахождение базы

      Чтобы найти базу с учетом шага и высоты, используйте формулу: где:
      L — длина отрезка
      A — высота

      Нахождение отрезка

      Чтобы найти длину ноги с учетом базы и высоты, используйте формулу: где:
      B — длина основания
      A — высота

      Высота

      Чтобы найти высоту по базе и ноге, используйте формулу: где:
      L — длина ножки
      B — основание
      

      Внутренние углы

      Если вам дадут внутренний угол равнобедренного треугольника можно найти два других.

      Например, нам дан угол при вершине, как показано справа от 40 °. Мы знаем, что внутренние углы всех треугольников составляют 180 °. Таким образом, два базовых угла в сумме должны составлять 180-40 или 140 °. Поскольку два основных угла совпадают (одна и та же мера), каждый из них составляет 70 °.

      Если нам дан базовый угол, скажем, 45 °, мы знаем, что базовые углы конгруэнтны (та же мера) а внутренние углы любого треугольника всегда складываются в 180 °. Таким образом, угол при вершине должен быть 180-45-45 или 90 °.

      Другие темы треугольника

      Общие

      Периметр / Площадь

      Типы треугольников

      Центры треугольника

      Конгруэнтность и сходство

      Решение треугольников

      Треугольник викторины и упражнения

      (C) Открытый справочник по математике, 2011 г.
      Все права защищены.

      .

      Добавить комментарий Отменить ответ

      Ваш адрес email не будет опубликован. Обязательные поля помечены *

      Комментарий *

      Имя *

      Email *

      Сайт